un vieux problème d'olympiade, je ne sais pas si vous avez déjà traité ça sur le forum :
Dans un plan on se donne un disque fermé de rayon 1, et on suppose qu'il contient 7 points dont les distances mutuelles sont toutes supérieures ou égales à 1. Prouver que le centre du disque est l'un de ces points.
7 points dans un disques
11 messages
- Page 1 sur 1
si on prend l'hexagone régulier inscrit dans le cercle, il se divise en 6 triangles équilatérales de coté 1,
soit un point dans une de ces portions(triangle ou non), pour faire du 1 faut aller , tomber sur la portion d'à coté, donc on pourra placer ainsi 6 points maxi,
il en manque 1,
reste plus que le centre et donc les 6 autres n'ont qu'à bien se tenir sur le cercle.
soit un point dans une de ces portions(triangle ou non), pour faire du 1 faut aller , tomber sur la portion d'à coté, donc on pourra placer ainsi 6 points maxi,
il en manque 1,
reste plus que le centre et donc les 6 autres n'ont qu'à bien se tenir sur le cercle.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
benekire2 a écrit:après bien sûr il n'y a plus qu'a écrire ça proprement, comme toujours ...
oui je crois qu'il faut écrire triangles équilatéraux et non pas équilatérales car c'est pas des gonzesses les triangles.
C'est pas propre ce que je raconte sinon?
Déjà qu'Imod a trouvé ça bète,
vais finir par me vexer ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Salut,
On désigne par les points considérés et par O le centre du cercle. Supposons par l'absurde qu'aucun de ces points n'est confondu en O. Alors le plus petit des angles
les points considérés et par O le centre du cercle. Supposons par l'absurde qu'aucun de ces points n'est confondu en O. Alors le plus petit des angles  est strictement inférieur à
est strictement inférieur à 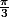 . Sans perte de généralité, supposons que cet angle minimum soit en les points
. Sans perte de généralité, supposons que cet angle minimum soit en les points  et
et 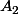 .
.
Or, d'après le théorème d'Al-Kashi,
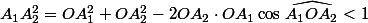
Contradiction !
On désigne par
Or, d'après le théorème d'Al-Kashi,
Contradiction !
beagle a écrit:mouais, c'est vraiment bête.
Ce n'était pas du tout une critique à ton égard , au contraire c'est très court , efficace et sans aucun calcul :++:
Il faut juste préciser qu'il peut y avoir deux points dans la même part ( au sens large ) mais qu'alors les points sont sur le cercle ou au centre du cercle :we:
Imod
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
