Pgcd
Olympiades mathématiques, énigmes et défis
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 14 Aoû 2006, 13:45
par raptor77 » 14 Aoû 2006, 13:45
Bonjour Soit n

2 un entier. Montrer qu'il n'existe pas d'entiers x,y

0 avec PGCD (x,n+1) et x

+1=y
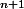
Bonne chance
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 14 Aoû 2006, 14:01
par aviateurpilot » 14 Aoû 2006, 14:01
PGCD(x,n+1)=?
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 14 Aoû 2006, 14:03
par raptor77 » 14 Aoû 2006, 14:03
aviateurpilot a écrit:PGCD(x,n+1)=?
PGCD(x,n+1)=1
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 14 Aoû 2006, 14:50
par aviateurpilot » 14 Aoû 2006, 14:50
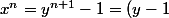(1+y+y^2+...+y^n))
si
=d)

divise

et d divise x
alors

divise
=1)
donc
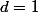
.
on pose
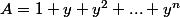
et
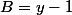
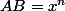
et
=1)
alors il existent a et b tel que
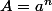
et

donc
^n)
donc

absurd
donc
 n'a pas de solution
n'a pas de solution
-
raptor77
- Membre Rationnel
- Messages: 813
- Enregistré le: 27 Mai 2006, 06:48
-
 par raptor77 » 14 Aoû 2006, 14:53
par raptor77 » 14 Aoû 2006, 14:53
bien :++: maintenant il te reste encore 2 exo :++:
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 14 Aoû 2006, 21:47
par El_Gato » 14 Aoû 2006, 21:47
aviateurpilot a écrit: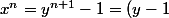(1+y+y^2+...+y^n))
si
=d)

divise

et d divise x
C'est sûrement une question stupide mais ca fait longtemps que j'ai pas fait d'arithmétique: pourquoi d divise n+1 ?
Merci
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 15 Aoû 2006, 09:24
par El_Gato » 15 Aoû 2006, 09:24
OK. Je me remettrais à l'arithmétique un de ces jours...
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 15 Aoû 2006, 11:53
par aviateurpilot » 15 Aoû 2006, 11:53
c'est bien
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
 2 un entier. Montrer qu'il n'existe pas d'entiers x,y
2 un entier. Montrer qu'il n'existe pas d'entiers x,y  0 avec PGCD (x,n+1) et x
0 avec PGCD (x,n+1) et x +1=y
+1=y