Bonjour voila une petite inégalité :
a,b,c > 0 et a+b+c=3 prouvez que
sum(1/a^2) >= sum(a^2)
et puis désolé pour le latex
Petite inégalité
14 messages
- Page 1 sur 1
par Olympus » 30 Nov 2010, 21:51
Salut et bienvenue !
J'ai une méthode un peu bourrin ( pas trouvé de méthode plus jolie pour le moment ) :
L'inégalité est équivalente à^4 \left( a^2b^2 + b^2c^2+c^2a^2 \right) \geq 81 a^2b^2c^2 \left( a^2 + b^2 + c^2 \right))
Mais il suffit de voir que par AM-GM ( à 34 termes ) :
On somme symétriquement et on a le résultat .
J'ai une méthode un peu bourrin ( pas trouvé de méthode plus jolie pour le moment ) :
L'inégalité est équivalente à
Mais il suffit de voir que par AM-GM ( à 34 termes ) :
On somme symétriquement et on a le résultat .
par darkpseudo » 30 Nov 2010, 22:33
Merci , mais vraiment pour être bourrin c'est bourrin . Au fait j'ai une question si a,b,c sont positifs et que 1/a+1/b+1/c >= a+b+c est ce qu'on ne peut pas en déduire l'inégalité , je dis ça par ce que le premier résultat est facile à démontrer .
par Olympus » 30 Nov 2010, 22:43
darkpseudo a écrit:Merci , mais vraiment pour être bourrin c'est bourrin . Au fait j'ai une question si a,b,c sont positifs et que 1/a+1/b+1/c >= a+b+c est ce qu'on ne peut pas en déduire l'inégalité , je dis ça par ce que le premier résultat est facile à démontrer .
Tu veux dire que tu veux appliquer cette dernière inégalité pas sur
par darkpseudo » 30 Nov 2010, 23:47
Non non je veux dire comment peut on exploiter cette inégalité pour prouver celle qu'il faut démontrer , je ne parle pas de changement de variable , je veux dire qu'on pourrais par exemple lever la première au carré et ensuite .... bein ensuite je bloque :)
par Olympus » 19 Déc 2010, 00:54
Bon j'ai trouvé une autre méthode horrible, mais plutôt analytique cette fois-ci ...
On pose
.
Vu que = \frac{1}{2} \left( \left( a-b\right)^2 + \left(b-c\right)^2+\left(c-a\right)^2 \right) \geq 0)
, il existe un réel positif 
tel que =q^2)
.
Donc})
.
Enfin, on pose
.
Notre inégalité est équivalente à
.
^2}{9}-6r)
 \leq \frac{\left(9-q^2\right)^2}{9})
On considère maintenant la fonction f définie par : = x^3 - \left(a+b+c\right)x^2 + \left(ab+bc+ca\right)x - abc = x^3 - 3x^2 + \frac{9-q^2}{3}x - r)
.
On a = 3x^2 - 6x + \frac{9-q^2}{3} = 3\left( x^2 - 2x + \left(1-\frac{q}{3}\right)\left(1+\frac{q}{3}\right) \right) = 3\left(x- 1 + \frac{q}{3} \right) \left( x- 1-\frac{q}{3} \right))
.
Donc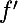
s'annule en 
et 
.
Donc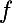
est croissante sur 
, et décroissante sur 
.
Il y a exactement une seule racine de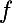 dans chaque intervalle ( 
, 
et 
), car sinon, on obtiendrait une contradiction vu qu'alors un des intervalles contiendrait au moins 2 racines par le principe de Dirichlet alors que 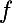est strictement monotone dans chacun des trois intervalles .
Sans perte de généralité, on suppose que
.
Donc par la décroissance de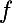 dans cet intervalle :  \leq f\left(a\right) \leq f\left( 1-\frac{q}{3} \right))
.
( remarquer que par construction,=0)
)
^2\left(3-2q\right) }{27} \leq r \leq \frac{ \left(3-q\right)^2\left(3+2q\right) }{27})
.
Il nous suffit donc de montrer que^2}{3+2q})
q + 225 - 3r \geq 0)
Mais^3 \leq \left( \frac{a+b+c}{3} \right)^3 =1)
, d'où la conclusion .
On pose
Vu que
Donc
Enfin, on pose
Notre inégalité est équivalente à
On considère maintenant la fonction f définie par :
On a
Donc
Donc
Il y a exactement une seule racine de
Sans perte de généralité, on suppose que
Donc par la décroissance de
( remarquer que par construction,
Il nous suffit donc de montrer que
Mais
par vincentroumezy » 19 Déc 2010, 10:56
Salut Olympus, tu ne serais pas un peu insomniaque, ou juste nerveux ? (à minuit);
Mais enfin, ce n'est pas l'objet de mon message.
Comment peut tu montrer que 1-6abc>=7/9 avec a+b+c=0 ?
Mais enfin, ce n'est pas l'objet de mon message.
Comment peut tu montrer que 1-6abc>=7/9 avec a+b+c=0 ?
par Olympus » 19 Déc 2010, 11:32
Salut !
Euh je ne sais pas comment le prendre :marteau:
Ton inégalité est fausse, prend = \left(-2;-1;3\right))
.
vincentroumezy a écrit:Salut Olympus, tu ne serais pas un peu insomniaque, ou juste nerveux ? (à minuit);
Euh je ne sais pas comment le prendre :marteau:
Comment peut tu montrer que 1-6abc>=7/9 avec a+b+c=0 ?
Ton inégalité est fausse, prend
par Olympus » 19 Déc 2010, 12:11
vincentroumezy a écrit:Pardon, avec a+b+c=1.
Je suppose que tes variables sont positives ( sinon il suffirait de prendre
Dans ce cas, ça se torche facilement par une simple application d'AM-GM .
Ou alors, on peut remarquer que :
Ou encore :
par vincentroumezy » 19 Déc 2010, 12:27
Joli, comment as tu pu atteindre une tlle maitrise des inégalités, entrainemen je suppose ?
par Olympus » 19 Déc 2010, 12:51
vincentroumezy a écrit:Joli, comment as tu pu atteindre une tlle maitrise des inégalités, entrainemen je suppose ?
Oui, en en travaillant des centaines avec les méthodes classiques ( AM-GM / Cauchy-Schwarz et Tchebyshev ), puis passage aux méthodes avancées ( réécriture sous forme de sommes de carrés, Schur, Muirhead, Mixing Variables et la méthode "PQR" ( celle que j'ai présenté ici avec les p,q et r ) ) .
Pour les méthodes classiques, le cours d'Animath suffit pleinement, pour les autres, il faudra passer un peu de temps sur Mathlinks et regarder comment les viet... euh membres torchent certaines inégalités bizarres ( y a pas mal de documents là-bas aussi ) :lol3:
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :