Périmètre bicolore

par **Imod** » 07 Juil 2010, 22:30

Bonsoir à tous :zen:

Une petite question que je me pose . On considère l'intersection de deux polygones réguliers , identiques à n côtés , un bleu et un rouge . On suppose que cette intersection est un polygone à 2n côtés . Chaque côté du polygone est un morceau d'un côté d'un des polygones de départ et prend sa couleur .

Il semble que les sommes des longueurs des segments bleus et des rouges soient les mêmes sur le périmètre du polygone .

Deux triangles équilatéraux :

Deux carrés :

Est-ce toujours vrai ?

Une idée :id:

Imod

par **nodjim** » 08 Juil 2010, 16:30

Imod a écrit:Il semble que les longueurs des segments bleus et rouges soient les mêmes sur le périmètre du polygone .

Bonsoir Imod,
Peux tu préciser: c'est "à chaque segment rouge correspond un bleu de longueur identique" ou "le total des longueurs des segments bleus est égal au total des longueurs des segments rouges" ou autre chose ?

par **Imod** » 08 Juil 2010, 16:41

Je parle de l'égalité de la somme des rouges avec la somme des bleus sur le périmètre du polygone jaune .

Imod

par **Ben314** » 09 Juil 2010, 08:42

Bon, c'est pas trés joli, mais ça a l'air de marcher :
Si tu calcule la variation de longueur d'un segment bleu créé par une petite translation du polygône bleu tu constate que la somme des longueurs bleues ne change pas lorsque l'on translate le polygône bleu (à condition qu'il y ait toujours le même nombre de points d'intersection).
Cela permet de se ramener au cas ou les deux polygônes ont même centre où le résultat est évident par symétrie.

par **beagle** » 09 Juil 2010, 09:34

Pas eu le temps de vérifier hier, je l'ai mis puis supprimer,
pas le temps ce matin , ni ce jour c'est la course,
donc attention ce message s'effacera dans x mn, y h.

Surface bleue qui déborde = surface rouge qui déborde
Tous les triangles qui débordent sont des triangles semblables.
Ils peuvent tous ètre des k fois, a,b, c d'un triangle de base, et mème h.
Donc somme des surfaces des triangles rouges= surface des triangles bleus
....
(k1+k'1+k"+...)c= (k2+k'2+k"2+...)c
somme des bases des triangles rouges 1 = somme des bases des triangles bleus 2
....

par **nodjim** » 09 Juil 2010, 16:08

Même conclusion, mais seulement si le polygone a un nombre pair de cotés. Je ne vois pas trop comment s'y prendre avec un nombre impair de cotés.

par **Ben314** » 09 Juil 2010, 17:31

Si tu note

un vecteur unitaire normal au k-ième coté du polygône bleu (orienté vers l'extérieur), alors une translation d'un vecteur

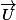
du polygône bleu modifie le k-ième segment bleu de

(produit scalaire) où

est une constante indépendante de k (car les triangles bleu "qui débordent" du polygône jaune sont tous semblables).
Comme la somme de vecteurs

est le vecteur nul, la somme des modif. des longueurs bleues dues à la translation est nulle.

P.S. : je vois pas où tu as eu besoin de différentier les paritées...

par **Imod** » 09 Juil 2010, 17:58

C'est aussi la méthode que j'ai utilisée mais je suis presque sûr qu'on peut faire plus rapide . Curieusement la somme des longueurs des segments bleus est égale à celle des rouges mais c'est aussi vrai pour la somme des aires des triangles qui s'appuient sur ces côtés ( et ils sont en effet tous semblables ) :doh:

Imod

par **nodjim** » 10 Juil 2010, 08:30

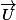
Ben314 a écrit:Si tu note un vecteur unitaire normal au k-ième coté du polygône bleu (orienté vers l'extérieur), alors une translation d'un vecteur du polygône bleu modifie le k-ième segment bleu de (produit scalaire) où est une constante indépendante de k (car les triangles bleu "qui débordent" du polygône jaune sont tous semblables).
Comme la somme de vecteurs est le vecteur nul, la somme des modif. des longueurs bleues dues à la translation est nulle.

P.S. : je vois pas où tu as eu besoin de différentier les paritées...

D'accord.
Avec un nombre pair de faces, les faces opposées sont parallèles, c'est plus facile à visualiser.

par **Ben314** » 10 Juil 2010, 22:52

Imod a écrit:C'est aussi la méthode que j'ai utilisée mais je suis presque sûr qu'on peut faire plus rapide . Curieusement la somme des longueurs des segments bleus est égale à celle des rouges mais c'est aussi vrai pour la somme des aires des triangles qui s'appuient sur ces côtés ( et ils sont en effet tous semblables ) :doh:

Imod

Pour les aires... ça ne me saute pas aux yeux (enfin, bref, j'ai pas trop cherché, j'ai pas trouvé, je chercherais plussss...)
Par contre (forcément !!!) je sais pas si on peut faire beaucoup plus court comme preuve pour les longueurs mais je serais preneur pour "plus joli" (i.e. sans faire de la vulgaire analyse beurk !!!)

par **Imod** » 11 Juil 2010, 08:51

Ben314 a écrit:Pour les aires... ça ne me saute pas aux yeux (enfin, bref, j'ai pas trop cherché, j'ai pas trouvé, je chercherais plussss...)

C'est que c'est trop évident :doh:

La somme des aires des triangles bleus ou celle des rouges est égale à l'aire du polygone de départ moins l'intersection :we:

Imod

par **Ben314** » 11 Juil 2010, 20:21

Imod a écrit:La somme des aires des triangles bleus ou celle des rouges est égale à l'aire du polygone de départ moins l'intersection :we:

Ch'uis vraiment trop c.. :cry:

par **Imod** » 12 Juil 2010, 14:28

Bon , en fait j'ai trouvé une démonstration utilisant uniquement le fait que les triangles extérieurs sont semblables . Je note a , b , c les côtés d'un triangle extérieur type , l le côté du polygone régulier et k1 , k2 , ... , k2n le taux d'agrandissement des triangles 1 , 2 , ... , 2n par rapport au modèle .

Sur chaque branche de l'étoile on a :

k1.a+k2.b+k2n.c=l
k2.a+k1.b+k3.c=l
k3.a+k4.b+k2.c=l
k4.a+k3.b+k5.c=l
...
k2n-1.a+k2n.b+k2n-2.c=l
k2n.a+k2n-1.b+k1.c=l

En comparant les sommes des rangs pairs et impairs on obtient :

(b+c-a)(k2+k4+k6+...+k2n)=(b+c-a)(k1+k3+k5+...+k2n-1)

Et c'est fini :we:

Imod

Périmètre bicolore

Périmètre bicolore

Qui est en ligne