Pavage du plan

[Zweig]

Est-il possible de recouvrir le plan par des cercles de sorte que par tout point passent exactement 1988 de ces cercles ?

[nuage]

A mon avis oui :
1988 est un nombre pair, et on peut recouvrir le plan par des cercles de telle sorte que par un point quelconque il passe 2 cercles...

[Zweig]

Euh, je n'ai pas compris ton raisonnement, on demande d démontrer que par tout point, si c'est possible (bon ça l'est en fait, mais faut le montrer), passent exactement 1988 de ces cercles et non 2 :marteau:

[_-Gaara-_]

Est-il possible de recouvrir le plan par des cercles de sorte que par tout point passent exactement 1988 de ces cercles ?

Salut,

Mais on peut toujours trouver un point par lequel ne passent pas 1988 cercles, non ? :hein:

je ne savais pas qu'on pouvait recouvrir un plan entièrement par des cercles XD

je n'ai rien pigé :hein:

[nuage]

Salut,
comme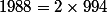 une fois qu'on a un recouvrement du plan par des cercles tq par chaque point passent deux cercles, il suffit de le recopier 994 fois avec un décalage judicieux à chaque copie.

je ne savais pas qu'on pouvait recouvrir un plan entièrement par des cercles XD

Un exemple : on prend deux points distincts A et B et on considère l'ensemble des cercles de centre A ou B : par chaque point du plan il passe au moins un des cercles de cet ensemble. Avec une remarque : on exclu souvent les cercles de rayon nul (point) ou infini (droite) dans les problèmes de ce type. Sinon c'est trop facile. Je pense que c'est le cas dans cet exercice.

[Imod]

je ne savais pas qu'on pouvait recouvrir un plan entièrement par des cercles XD

Recouvrir n'est pas partitionner , en considérant tous les cercles du plan tu le recouvre aisément :zen:

Imod

PS : le partitionnement est impossible .

[_-Gaara-_]

Merci Imod et nuage, je viens de comprendre ! :D

En fait si le nombre de cercles était impair on y arriverait pas, c'est bien celà ?

[nodgim]

On parle de cercles ou de disques, là?

[nuage]

Salut

On parle de cercles ou de disques, là?

on parle de cercles : cercle de centre A et de rayon r : ensemble des points situé à une distance r de A

[nuage]

Salut Imod

Recouvrir n'est pas partitionner , en considérant tous les cercles du plan tu le recouvre aisément :zen:

Imod

PS : le partitionnement est impossible .

Le partitionnement est possible, mais guère intéressant, si on admet un cercle de rayon nul.

[Imod]

Salut Imod

Le partitionnement est possible, mais guère intéressant, si on admet un cercle de rayon nul.

Comme quoi dans tous ces exercices il faudrait préciser les termes ambigus : plan euclidien , cercle de rayon non nul ( ça devient vite un peu lourd :marteau: )

Imod

[nuage]

Comme quoi dans tous ces exercices il faudrait préciser les termes ambigus : plan euclidien , cercle de rayon non nul ( ça devient vite un peu lourd :marteau: )

Imod

Je suis d'accord.
Et j'ai pris l'exercice de départ dans ce sens.
mais je pense quand même qu'il vaut mieux préciser les choses dans ce genre de problème. :briques:
Avec mes excuses
nuage :

[nodgim]

Dans un plan, on peut dessiner autant de cercles que l'on veut qui passent par un point donné. En aucun cas, on ne peut limiter ce nombre.