Partition | Probleme NP | Difficile

[reikon]

Bonjour,

Je me permets de vous présenter un problème mathématique auxquel je suis confronté actuellement
dans ma profession.

Imaginez que vous ayez une pile de 200 cailloux de masses differentes et 28 brouettes de capacité identiques.
Comment répartir ces cailloux dans ces brouettes, en gardant l'écart entre les brouettes le plus minimal possible.

Je me permets d'ajouter qu'un jour il y aura 200 cailloux et 28 brouettes, et qu'un autre jour ces nombres peuvent varier.

J'éspère avoir été clair !

En vous souhaitant bien du courage.

Cordialement,
ReiKon

[Cliffe]

l'écart entre les brouettes

l'écart de quoi ? le poids ?

tu veux minimiser la somme des écarts entre chaque brouette ?

[reikon]

l'écart de quoi ? le poids ?

tu veux minimiser la somme des écarts entre chaque brouette ?

Je souhaiterai que les brouettes aient un pied similaire, le plus proche possible les unes des autres. Je souhaite trouver la meilleure solution de réparation.

[Cliffe]

c'est quoi le pied d'une brouette ?

[reikon]

c'est quoi le pied d'une brouette ?

Poids si tu préfères. Ou mieux, masse. Le défi n'est pas adapté?

[Cliffe]

tu peux écrire un programme linéaire et le résoudre avec un solveur.

[reikon]

tu peux écrire un programme linéaire et le résoudre avec un solveur.

Mais encore? Je précise que je ne cherche pas une approximation ou une solution, mais la solution la meilleure possible.

[Cliffe]

ça dépend du critère de minimisation que tu choisis.
le plus simple c'est de faire la somme des écarts.

exemple, si je note le poids de la i-ème brouette, alors on cherche :

[CENTER][/CENTER]



on peut aussi utiliser le poids moyen et s'en approcher au mieux. A toi de voir.

[Cliffe]

j'ai eu le temps de réfléchir un peu, voila le programme qui te donnes la solution exacte :

Données :
- Soit le nombre de cailloux
- le poids (ou masse ) du i-ème cailloux.
- Soit le nombre de brouettes.

Variables de décisions :
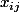- égale à 1 si le i-ème cailloux est dans la j-ème brouette.
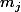- le poids de la j-ème brouette.

Programme linéaire :
[CENTER]
[/CENTER]

[chaikov]

Imaginez que vous ayez une pile de 200 cailloux de masses differentes et 28 brouettes de capacité identiques.
Comment répartir ces cailloux dans ces brouettes, en gardant l'écart entre les brouettes le plus minimal possible.

Comme l'a dit Cliffe, la moyenne du poids des cailloux est l'objectif visé. Idéalement, toutes les brouettes contiendraient exactement le même poids, qui serait le poids moyen des cailloux.

Les cailloux les plus lourds sont les moins 'flexibles', alors que les cailloux légers permettent un ajustement fin du poids dans chaque brouette. On répartira donc d'abord les cailloux lourds, les cailloux légers permettant ensuite d'ajuster le poids des brouettes de la façon le plus égale possible.

En fin de répartition, il faudra envisager d'échanger des cailloux entre la plus lourde et la plus légère des brouettes, et répéter ce type d'échange jusqu'à obtention du niveau d'uniformité désiré.

La somme des carrés des écarts à la moyenne est le critère normalement retenu pour estimer la variabilité d'une répartition. (et non pas la somme des valeurs absolues des écarts, telle que recommandée par Cliffe, qui présente le défaut de sous-évaluer l'importance des grands écarts)

[Cliffe]

oui les écarts aux carrées. J'ai juste donné un exemple ...

Le modèle que j'ai donné ensuite permet de résoudre le pb grâce à la programmation linéaire.
L'idée est de trier les brouettes par poids. La première étant la plus légère et la dernière la plus lourde : .
Ensuite il suffit de minimiser la fonction objectif : .