Partie entière
Olympiades mathématiques, énigmes et défis
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 05 Juin 2007, 12:10
par mt2sr » 05 Juin 2007, 12:10
bonjour
je vous propose l'exercice suivant
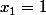

calculer
)
je pense que pour n>=4 E(xn^2)=n j'ai pas encore démontré le résultat
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 05 Juin 2007, 12:27
par aviateurpilot » 05 Juin 2007, 12:27
oui c'est bien
^2]=n)
il suffit de montrer par recurrence que
^2}{n}-1\|<\frac{1}{n-1})
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 05 Juin 2007, 13:16
par mt2sr » 05 Juin 2007, 13:16
merci pour l'indication
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 06 Juin 2007, 13:01
par mt2sr » 06 Juin 2007, 13:01
cette inégalité est insufisante pour déduire le résultat
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 06 Juin 2007, 13:20
par aviateurpilot » 06 Juin 2007, 13:20
mt2sr a écrit:cette inégalité est insufisante pour déduire le résultat
dsl, j'ai pas fait attention,
voila le resultat que tu dois montrer

-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 06 Juin 2007, 13:48
par mt2sr » 06 Juin 2007, 13:48
encor insuffisant je crois quand dois remplacer 1/(n-1) par 1/(n+1)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 06 Juin 2007, 14:03
par aviateurpilot » 06 Juin 2007, 14:03
je postrai ma solution apres avoir manger klk chose, ok :++:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 06 Juin 2007, 19:23
par Imod » 06 Juin 2007, 19:23
Attention à l'indigestion :we:
Imod
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 06 Juin 2007, 19:39
par fahr451 » 06 Juin 2007, 19:39
et l'exo de dénombrement que tu m'as demandé aviateur pilote ?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 06 Juin 2007, 19:55
par aviateurpilot » 06 Juin 2007, 19:55
Imod a écrit:Attention à l'indigestion :we:
Imod
:ptdr: :ptdr:
fahr a écrit:et l'exo de dénombrement que tu m'as demandé aviateur pilote ?
ok
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 08 Juin 2007, 09:07
par mt2sr » 08 Juin 2007, 09:07
bonjour personne n'a une idée pour le pb
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 08 Juin 2007, 11:17
par aviateurpilot » 08 Juin 2007, 11:17
soit
=\frac{x}{n}+\frac{n}{x}\ (decroissante\ sur\ ]0,n]))
soit

donc on a
:a_n>\sqrt{n}\ et\ (2):a_n\ge \frac{n-1}{\sqrt{n-2}})
avec un changement de variable dans
)
on a aussi

.
et donc
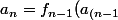+1})\le f_{n-1}(\frac{n-2}{\sqrt{n-3}})a_n>\sqrt{n})
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 09 Juin 2007, 12:18
par mt2sr » 09 Juin 2007, 12:18
merci je vais etudier votre raisonnement
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités