Partie entiere/parité

[lapras]

Salut,
trouver , :
, ,

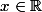
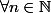
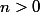
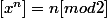
Lapras

[ffpower]

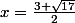
semble marcher..Voila pour la reponse brute,je peux mettre la demo si vous voulez(et eventuellement le raisonnement)

[charlol]

je veux bien que tu donnes les 2 ^^

[ffpower]

dsl,j ai fait mon malin,mais en fait je crois que j ai une erreur de raisonnement..

[ffpower]

bon j avais bien fait une erreur de raisonnement,et en le rectifiant,je tombe sur..le meme resultat lol.donc ca marcheen fait(je viens de texter a la calto^^)

[lapras]

oué ca marche bien !
l'idée principale (je suis sur que c'est ton idée), c'est de penser aux suites linéaires entieres de la forme x^n + y^n avec |y| < 1, on peut ensuite calculer la partie entiere ;)

[ffpower]

tu lis en moi comme dans un livre ouvert lol...C est sur que je vois pas trop d autres pistes en fait lol.Etudier la parité que la suite x^n+y^n en fonction de la parité de la somme S et du produit P,les conditions que doivent vérifier S et P pour que x>1 et |y|<1,regarder la parité de [x^n] qui se compare a celle de x^n+y^n selon le signe de y,puis choisir S et P(minimaux) pour que tout marche bien..c était amusant en tout cas.Je me demande si on peut déterminer l ensemble des x qui marchent(en particulier sont ils forcément algébrique de degré 2?).C est p-e un probleme difficile ca,je sais pas trop...