[Défi TS] Oral des Mines

[Zweig]

Salut,

Un exercice où les TS vont pouvoir se casser les dents ...

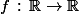
Déterminer toutes les fonctions , dérivables en 0 et vérifiant :

[CENTER][/CENTER]

Bonne chance !

[Le_chat]

Petites mines? j'ai bien une solution mais elle utilise la densité de Q dans R...
PS: vu que c'est faisable en TS, me suis surement compliqué la vie :ptdr: mais sa marche.

[Zweig]

Non non, des Mines. Donne toujours :zen:.

[Le_chat]

Voila:
Alors d'abord on montre facilement que f(x)>0 ou que f est la fonction nulle.
Ensuite, une récurrence immédiate pour montrer que pour tout "n" naturel f(2n)=(f(1))^2n, et de même pour tout naturel non nul "q" f(1/(2q))=(f(1))^1/(2q).
On prouve par deux autre petites récurrences successives que
f(n/q)=f(2n/2q)=(f(2n))^(1/2q)=(f(1))^(n/q).
Donc pour tout rationnel "p",f(p)=(f(1))^p.
Apres pour tout x réel, on sort une suite Un de rationnels convergente vers x (Un existe car Q est dense dans R!).
f(Un)=(f(1))^Un comme démontré précédemment. D'après la caractérisation séquentielle de la limite, lim en x de f(x)=lim de f(Un)=(f(1))^x.
RÉCIPROQUEMENT , de telles fonctions sont solutions.
Je ne suis pas très sur de la justesse de ma démo, mais le raisonnement doit y être. Après, vu que c'est un défi pour des TS, je pense que sa doit être faisable bien moins lourdement.

[Zweig]

Si j'ai bien compris, tu trouves que les solutions sont , c'est ça ? En fait, on peut être plus précis. On montre que les fonctions solutions sont la fonctionne nulle et les fonctions

[Le_chat]

Bien non n'est pas constante (on a bien solution, et donc
Edit ( a la vue de ton edit) c'est bien ce que j'ai trouvé. Si , alors f(1)=a et on a bien le même resultat.

[Zweig]

(Oui je sais, j'ai édité juste après avoir vu ma bourde :marteau:)

[Zweig]

Mais il reste à faire la réciproque maintenant, montrer que

[Zweig]

Ta solution a le mérite d'être plus courte que celle niveau lycée :zen:

[Le_chat]

Bien si f est solution de l'équation fonctionnelle, j'ai montré (ou du moins je crois avoir montré :we: ) que .
Réciproquement, ces fonctions vérifient bien l'équation fonctionnelle, donc toutes les solution de l'équation fonctionnelle sont les fonctions qui a x associent a^x avec 0;)a

[Le_chat]

Je serai curieux de voir la solution niveau lycée. Il y a une astuce ou il s'agit d'une méthode marchant pour différentes équations fonctionnelles?
(plutôt par Mp, si cela ne dérange pas, pour laisser chercher les lycéens.)

[Zweig]

Elle utilise une technique réutilisable dans pas mal d'équations fonctionnelles. La technique peut être vue en effet, au début quand on ne la connait pas, comme une astuce ... En fait, elle ne sort pas de n'importe où : elle n'est qu'une conséquence de la recherche de la mise en action de l'hypothèse "dérivable (donc continue) en 0".

Patiente 5min, je rédige ça en un fichier PDF et je le poste.

[girdav]

Voila:
Alors d'abord on montre facilement que f(x)>0 ou que f est la fonction nulle.
Ensuite, une récurrence immédiate pour montrer que pour tout "n" naturel f(2n)=(f(1))^2n, et de même pour tout naturel non nul "q" f(1/(2q))=(f(1))^1/(2q).
On prouve par deux autre petites récurrences successives que
f(n/q)=f(2n/2q)=(f(2n))^(1/2q)=(f(1))^(n/q).
Donc pour tout rationnel "p",f(p)=(f(1))^p.
Apres pour tout x réel, on sort une suite Un de rationnels convergente vers x (Un existe car Q est dense dans R!).
f(Un)=(f(1))^Un comme démontré précédemment. D'après la caractérisation séquentielle de la limite, lim en x de f(x)=lim de f(Un)=(f(1))^x.
RÉCIPROQUEMENT , de telles fonctions sont solutions.
Je ne suis pas très sur de la justesse de ma démo, mais le raisonnement doit y être. Après, vu que c'est un défi pour des TS, je pense que sa doit être faisable bien moins lourdement.

Je ne sais pas si le passage par la continuité séquentielle ne peut pas se justifier autrement.
Ici, rien ne dit que la fonction est continue en dehors de .
Comment le justifies-tu?

[Le_chat]

Je ne sais pas si le passage par la continuité séquentielle ne peut pas se justifier autrement.
Ici, rien ne dit que la fonction est continue en dehors de .
Comment le justifies-tu?

Et paf! ma demo tombe a l'eau

[gdlrdc]

Commence par écarter le cas f = 0,
Puis facilement on montre que f est > 0 et f(x) = ( f ( x/2^n) )^(2^n)
Puis on passe au log et on appelle g = ln(f)
g est dérivable en 0 et on montre que g est dérivable sur R et que g' est constante.... et le tour est joué en intégrant et en passant à l'exponentielle.
Ca me semble bon, y a peut-être plus court

[Zweig]

Salut,

J'ai fait exactement pareil à ceci près que je n'ai pas montré que g était dérivable sur \mathbb{R}. Pour résoudre g(x) = 2g(x), j'ai introduit une fonction auxiliaire, h(x) = g(x)/x si x différent de 0, g'(0) sinon ; On a h dérivable en 0 et h(2x) = 2h(x). On montre h(x) = h(0), i.e, h constante.

[benekire2]

euh ... j'ai fais l'exercice ( enfin là de tête) et a première vue, j'aurais dit que les solutions étaient avec lambda et a réels les fonctions :

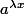
quelqu'un pourrait me dire où est mon erreur ? Merci.

[Le_chat]

euh ... j'ai fais l'exercice ( enfin là de tête) et a première vue, j'aurais dit que les solutions étaient avec lambda et a réels les fonctions :

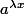
quelqu'un pourrait me dire où est mon erreur ? Merci.

Tu as trouvé les bonnes soltions, mais on peut simplifier: a^(lx)=(a^l)^x donc en posant T=a^l tu trouves bien que toutes les solutions sont T^x.

[Nightmare]

Je ne sais pas si le passage par la continuité séquentielle ne peut pas se justifier autrement.
Ici, rien ne dit que la fonction est continue en dehors de .
Comment le justifies-tu?

En fait on peut justifier en remarquant que :

et évaluer pour n assez grand.

[Ben314]

Par rapport au problème de départ, ne serait il pas plus simple de se rammener en 0 où, par hypothèse f est dérivable (donc continue) ?

Si , en faisant tendre vers l'infini, il n'y as pas d'indétermination et on obtient .
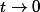
Sinon, c'est que (car ) et on a avec lorsque d'où :
si
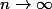
(cette dernière étape étant sans doute à détailler niveau T.S.)