soit f une application de N* dans N, vérifiant les propriétés suivantes :
-quelque soit m et appartenant à N* , f(m+n)-f(m)-f(n) prend l'une des valeurs 0 ou 1 :
-f(2)=0, f(3)>0 et f(9999)=3333
déterminer f(1982). merci
Olympiades mathématiques
11 messages
- Page 1 sur 1
new007 a écrit:soit f une application de N* dans N, vérifiant les propriétés suivantes :
-quelque soit m et appartenant à N* , f(m+n)-f(m)-f(n) prend l'une des valeurs 0 ou 1 :
-f(2)=0, f(3)>0 et f(9999)=3333
déterminer f(1982). merci
salut
une idée de recherche seulement
soit une suite f vérifiant les conditions de l'énoncé
f(2)-f(1)-f(1)=-2f(1) ne peut pas être égal à 1 donc f(1)=0
f(3)-f(1)-f(2)=f(3) donc f(3)=1
donc
f(1)=0
f(2)=0
f(3)=1
f(n)-f(n-1)-f(1)=f(n)-f(n-1)= 0 ou 1
f(n)-f(n-2)-f(2)=f(n)-f(n-2)=0 ou 1
f(n)-f(n-3)-f(3)=f(n)-f(n-3)-1=0 ou 1 soit f(n)-f(n-3)=1 ou 2
si on considère les termes d'une suite f(n)
ils augmentent à chaque fois de 0 ou 1
si deux termes consécutifs sont différents, il n' y a pas augmentation
si trois termes consécutils sont égaux, il y a augmentation de 1
si on décide d'augmenter le moins possible à chaque fois on définit la suite des f(i) à partir de i=1:
0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5,
Soit donc la suite g définie par (pour tout entier non nul k)
g(1)=g(2)=0
g(3k)=k
g(3k+1)=k
g(3k+2)=k
on a bien g(9999)=3333
alors g(1980)=660
g(1981)=660
g(1982)=660
g(1983)=661
On démontre facilement que cette suite g satisfait les hypothèses de l'énoncé.
SI on démontre que g est la seule suite qui satisfait l'énoncé, c'est terminé :hum:
On peut généraliser un peu l'énoncé initial :
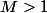 est un entier positif,
est un entier positif, ) est une suite d'entiers positifs ou nuls, telle que
est une suite d'entiers positifs ou nuls, telle que \geq f(m)+f(n) ,\ f(3)>0,\ f(3M)=M)
Il est facile de voir que\geq f(n)+f((m-1)n)\geq ..\geq mf(n))
On écrit\geq kf(3)) , donc
, donc \leq f(3M)=M) et comme
et comme 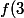) est un entier positif on a
est un entier positif on a 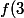=1) , donc
, donc \geq k)
Pour tout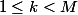 on a
on a \geq f(3k)+f(3(M-k))\geq f(3k)+(M-k)) donc
donc \leq k)
Il s'ensuit que pour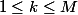 on obtient
on obtient =k) .
.
D'autre part on a\geq 3f(k)) d'ou
d'ou \leq \frac k3)
On a donc\leq \frac 13,\ 0\leq f(2)\leq \frac 23) , d'où
, d'où =f(2)=0)
Pour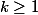 et
et 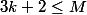 on a
on a \leq f(3k+1)\leq f(3k+2)\leq \frac {3k+2)}3\) , et on obtient :
, et on obtient :
=f(3k+1)=f(3k+2)=k) ou encore
ou encore =[\frac n3]) (partie entière) .. (q.e.d)
(partie entière) .. (q.e.d)
:zen:=660) :zen:
:zen:
Il est facile de voir que
On écrit
Pour tout
Il s'ensuit que pour
D'autre part on a
On a donc
Pour
:zen:
MMu a écrit:On peut généraliser un peu l'énoncé initial :est un entier positif,
est une suite d'entiers positifs ou nuls, telle que
Il est facile de voir que\geq f(n)+f((m-1)n)\geq ..\geq mf(n))
On écrit, donc
et comme
est un entier positif on a
, donc
Pour touton a
donc
\leq k)
Il s'ensuit que pouron obtient
.
D'autre part on ad'ou
On a donc
Salut
on ne peut pas changer l'énoncé en faisant intervenir un M mal défini :hum:
MMu a écrit:C'est si difficile de voir la généralisation ? :hum:
Bravo pour ta démo :++:
Je doute un peu pour M=2 cependant
si tu considères la suite
f(1)=0
f(2)=0
f(3)=1
f(4)=1
f(5)=2
f(6)=2
soit 0,0,1,1,2,2,3,3,4,4,5,5,6,6, ... f(2k+1)=k et f(2k)=k-1
donc avec M=2
on a f(3M)=M et f(5) n'est pas égal à 1
cette suite vérifie pourtant les hypothèses
D'avance mes excuses si j'ai fait une ânerie :zen:
chan79 a écrit:Bravo pour ta démo :++:
Je doute un peu pour M=2 cependant
si tu considères la suite
f(1)=0
f(2)=0
f(3)=1
f(4)=1
f(5)=2
f(6)=2
soit 0,0,1,1,2,2,3,3,4,4,5,5,6,6, ... f(2k+1)=k et f(2k)=k-1
donc avec M=2
on a f(3M)=M et f(5) n'est pas égal à 1
cette suite vérifie pourtant les hypothèses
D'avance mes excuses si j'ai fait une ânerie :zen:
Salut chan79, ..
Dans ma démo on voit que
MMu a écrit:Pouret
on a
, et on obtient :
ou encore
(partie entière) ..
Si M=2 tu ne peux pas avoir k>=1 et 3k+2<=M, donc on peut rien conclure
les deux suites suivantes vérifient les hypothèses initiales avec f(6)=2
00111222333444555
00112233445566778
mais pas de souci, si f(9999)=3333, alors f(1982) est bien égal à 660, comme tu l'as parfaitement démontré :zen:
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
