Olympiade mathématique

[M@thIsTheBest]

Voilà une question proposée dans l'olympiade international de mathématique 2006:
Trouver tous les couples (x,y) (x et y éléments de ) tq :
.
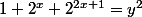
voilà deux solutions particulières:
(0,2) et (0,-2).

[M@thIsTheBest]

Pas de réponses ?

[Dinozzo13]

Voilà une question proposée dans l'olympiade international de mathématique 2006:
Trouver tous les couples (x,y) (x et y éléments de ) tq :
.
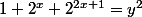
voilà deux solutions particulières:
(0,2) et (0,-2).

Salut !

Tu cherches les solutions ou tu nous proposes cet exercice en tant que défi ?

Déjà

Je ne parviens pas à la résoudre , toutefois, résoudre cette équation revient à résoudre :
.

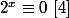
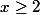
Après je ne suis pas sûr, mais on peut peut-être exploiter le faitr que que pour , on a :
.
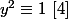
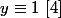
Or ssi ou .

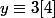
[manoa]

Je ne parviens pas à la résoudre , toutefois, résoudre cette équation revient à résoudre :
.

euh, plutôt :we:

[Matt_01]

On réécrit de cette manière :

Deux possibilités :
avec impair (on regarde les valuations 2-adiques) (On suppose y,x > 0)
Alors : .
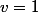
Mais, par simple comparaison de grandeur, ceci implique avec ou pour plus de rapidité

[M@thIsTheBest]

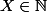
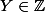
Je doit d'abord corriger l'énoncé: (ne pose pas de problème car si x<0 il n'y a pas de solutions) mais .( la remarque de Dinozzo13 est très importante)
Et félicitation à Matt_01 puisque il a trouvé" le fil d'Ariane".
Alors les solutions sont (0,2);(0,-2);(4;23) et (4;-23).
Et voilà la démonstration la plus exacte + les autres énoncés:http://www.cms.org.cn/cms/news/2006/20060718-2.pdf