Olympiade Mathématique:arithmétique et algèbre

[M@thIsTheBest]

Bonjour,
2 exercice à résoudre et svp je veux la démonstration complète:
1-n est un entier naturel impair.Déterminer m et n tel que
2-a,b,c sont des entiers naturels non nuls. Déterminer a,b,c tel que .
merci d'avance.

[miss mathe]

bon soir

y a pas des informations sur "m" dans que-1 ?

[nodjim]

Pour la 2) c'est pas plutôt 1/b² une fois ?

[MMu]

Bonjour,
2 exercice à résoudre et svp je veux la démonstration complète:
1-n est un entier naturel impair.Déterminer m et n tel que
2-a,b,c sont des entiers naturels non nuls. Déterminer a,b,c tel que .
merci d'avance.

1)
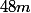
Il faut que divise et comme est impair il faut que divise :

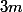
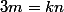
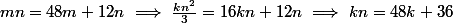
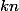
doit diviser et comme est impair on a
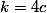
donc
Il faut donc que divise :







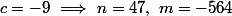
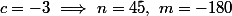
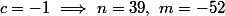
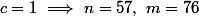
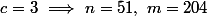
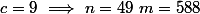
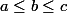
2) Supposons . On observe :
Tous les nombres doivent être supérieurs à , donc
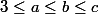
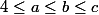
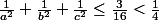
Si on a , il faut donc .
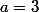
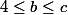
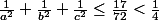
Si alors , il faut donc .
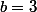
L'équation devient
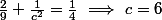
Bien-sur, toute permutation des valeurs fait l'affaire .
:zen:

[M@thIsTheBest]

1)
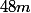
Il faut que divise et comme est impair il faut que divise :

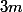
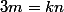
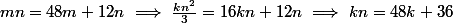
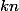
doit diviser et comme est impair on a
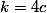
donc
Il faut donc que divise :







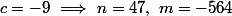
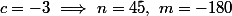
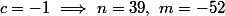
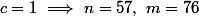
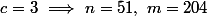
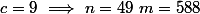
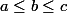
2) Supposons . On observe :
Tous les nombres doivent être supérieurs à , donc
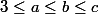
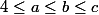
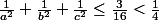
Si on a , il faut donc .
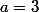
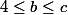
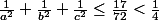
Si alors , il faut donc .
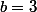
L'équation devient
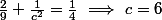
Bien-sur, toute permutation des valeurs fait l'affaire .
:zen:

Merci bien, bonne raisonnement...

[nodjim]

Oui bon aussi si on écrit direct les solutions, y a plus de suspens..

[miss mathe]

1)
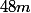
Il faut que divise et comme est impair il faut que divise :

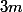
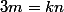
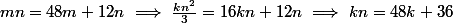
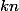
doit diviser et comme est impair on a
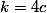
donc
Il faut donc que divise :







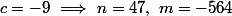
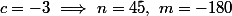
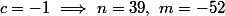
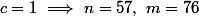
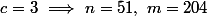
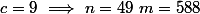
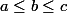
2) Supposons . On observe :
Tous les nombres doivent être supérieurs à , donc
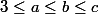
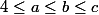
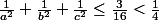
Si on a , il faut donc .
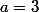
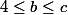
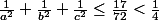
Si alors , il faut donc .
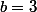
L'équation devient
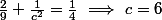
Bien-sur, toute permutation des valeurs fait l'affaire .
:zen:

tu es géni :doh: chapeau bas