Oeil

par **Zweig** » 10 Juil 2012, 17:20

Salut,

Etant donnés un rectangle de longueur L et de largueur l, et 5 cercles bleus de même rayon, déterminer L/l.

http://www.noelshack.com/2012-28-1341937224-oeil.png

par **nodjim** » 10 Juil 2012, 17:37

Ah, ces problèmes japonais....

par **Kikoo <3 Bieber** » 10 Juil 2012, 18:46

C'est plutôt 5 cercles bleus de même rayon, non ? ^^

Rolala, pas facile vos défis géométriques... :triste: Je vais essayer de les physiquifier.

par **chan79** » 10 Juil 2012, 19:41

Zweig a écrit:Salut,

Etant donnés un rectangle de longueur L et de largueur l, et 5 cercles bleus de même rayon, déterminer L/l.

http://www.noelshack.com/2012-28-1341937224-oeil.png

Je trouve

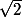
Ah, ce brave Pythagore !

par **acoustica** » 10 Juil 2012, 19:44

par **C.Ret** » 10 Juil 2012, 20:27

La largeur (en fait la hauteur sur la figure), ce ne sera pas

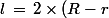avec respectivement

rayon des deux grands cercles noirs et

rayon des cinq petits cercles ?

par **chan79** » 10 Juil 2012, 22:14

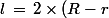C.Ret a écrit:La largeur (en fait la hauteur sur la figure), ce ne sera pas avec respectivement rayon des deux grands cercles noirs et rayon des cinq petits cercles ?

Les deux grands cercles ont comme rayon L/2
si r est le rayon du cercle central, L/2+L/2=l+2r
r=(L-l)/2

par **Imod** » 10 Juil 2012, 23:17

Le problème est assez simple quand on a repéré le carré :zen:

Un problème qui m'avait inspiré un gâteau il y a peu .

Imod

Oeil

Oeil

Qui est en ligne