Non-monotonie facile et sympa

[MMu]

Soient deux fonctions , intégrables, telles que.
Montrer qu'au moins une des fonctions n'est pas strictement monotone.

[Ben314]

Salut,
On procède par l'absurde en supposant qu'il existe deux fonctions et de [0,1] dans intégrables, strictement monotone et telles que
On vérifie aisément que, si un couple de fonction vérifie alors, pour tout le couple vérifie aussi .
En remplaçant par avec on peut donc supposer que est strictement croissante et que et dans ce cas, l'égalité signifie que .
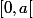
Vu la stricte croissance de et le fait que son intégrale est nulle, il existe un (unique) tel que sur et sur .
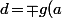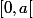
En remplaçant par avec on peut aussi supposer que est strictement croissante et que ce qui implique que sur et sur .
Sauf qu'on a alors sur ce qui est contradictoire avec le fait que .