Ce nombre ne peut pas valoir 33.
Olympiades mathématiques, énigmes et défis
-
aviateur
 par aviateur » 20 Mar 2018, 19:02
par aviateur » 20 Mar 2018, 19:02
Bonjour
Pour animer un peu le forum voici une question à la portée de tous (du point de vue connaissances) mais pas aussi facile que ça à résoudre.
Soit
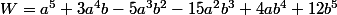
où

et

sont des entiers.
Montrer que
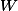
ne peut pas prendre la valeur
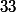

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 20 Mar 2018, 21:10
par chan79 » 20 Mar 2018, 21:10
salut
Ca se factorise pas mal
-5a^2 b^2(a+3b)+4b^4(a+3b)=(a+3b)(a^4-5a^2b^2+4b^4))
la parenthèse de droite s'annule pour

et pour
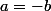
on la divise par

et on arrive à
(a+b)(a-b)(a-2b)(a+2b))
il faut voir si un facteur peut être égal à 33 et le produit des autres à 1 et de même avec -33 et -1, avec 3 et 11 etc
Un programme peut aider.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 21 Mar 2018, 08:56
par Dacu » 21 Mar 2018, 08:56
aviateur a écrit:Bonjour
Pour animer un peu le forum voici une question à la portée de tous (du point de vue connaissances) mais pas aussi facile que ça à résoudre.
Soit
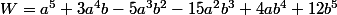
où

et

sont des entiers.
Montrer que
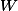
ne peut pas prendre la valeur
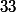
Bonjour,
Nous remarquons que
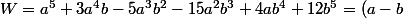(a+b)(a-2b)(a+2b)(a+3b))
.
Nous remarquons aussi que
(a+b)(a-2b)(a+2b)(a+3b)=33)
seulement si
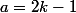
et
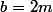
, ce qui signifie que
(a+b)(a-2b)(a+2b)(a+3b)=n\cdot p\cdot r \cdot s\cdot t=1\cdot 3\cdot 11)
unde
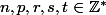
sont des nombres impairs.Nous devons voir toutes les combinaisons possibles pour lesquelles
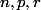
ou
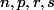
, par exemple, peuvent être égaux à

ou

. Enfin, il s'ensuit que
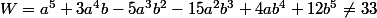
pour tout
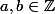
.
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
aviateur
 par aviateur » 21 Mar 2018, 09:34
par aviateur » 21 Mar 2018, 09:34
Bonjour
Oui la solution passe bien par la factorisation de W.
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 21 Mar 2018, 10:33
par beagle » 21 Mar 2018, 10:33
des entiers il n' y en a pas beaucoup,
donc a= 0 donne d'emblée 12b^5 je cherche même pas b
ensuite grace à chan79,
a=b donne zéro
donc faut prendre a différent b
avec b= 2 on va avoir plus que 6x2x4 déjà on passe pas en dessous
reste donc b=1 et a= 2 à chercher qui fait encore plus que 5x3x4, toujours pas en dessous
bref même on baissant la tète y a rien qui passe en dessous.
c'est pas terrible pour expliquer pourquoi 33, mais bon!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
aviateur
 par aviateur » 21 Mar 2018, 11:35
par aviateur » 21 Mar 2018, 11:35
Bonjour
Si on part de la factorisation de Dacu:
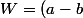(a+b)(a-2b)(a+2b)(a+3b)=33)
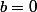
n'est manifestement pas une solution. Alors pour tout
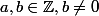
on a que
33 est un produit de 5 facteurs différents 2 à 2.
Or les décompositions possibles de 33 en facteurs différents sont:
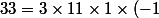)
ou
\times (-11) \times 1 \times (-1))
mais je n'arrive pas à mettre un 5 ème facteur!!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
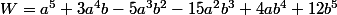
et
sont des entiers.
ne peut pas prendre la valeur