Niveau terminale S ++
Olympiades mathématiques, énigmes et défis
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 17 Avr 2006, 17:55
par Mikou » 17 Avr 2006, 17:55
Voila je ne sais pas trop ou poster cela, ca ne convient pas a la section cafe maths ny enigme, je propose donc ici un exo pour niveau d'un assez bon terminale, un peu demulation en fait pas de mal hein :happy3:
Avant tt chose je precise,que comme les differents sujets a venir,celui ci n'est pas de moi mais d'un certain 'Bouzard', merci a lui :happy3:
Exercice : On définit pour

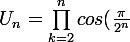)
Montrer que la suite u converge.
Maintenant considérons
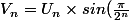)
Montrer que la suite v est géométrique et en déduire le terme général de la suite u
-
nimitz
- Membre Naturel
- Messages: 48
- Enregistré le: 09 Jan 2006, 19:22
-
 par nimitz » 18 Avr 2006, 17:19
par nimitz » 18 Avr 2006, 17:19
Soit
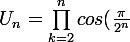)
pour tout

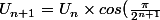)
On a:

Or sur l'intervalle

, la fonction cosinus est strictement décroissante, d'où
 > cos(\frac{\pi}{2^{k+1}}) > cos(\frac{\pi}{2}))
soit
 > 0)
donc
<1)
On en déduit donc que donc
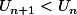
La suite
)
est donc strictement décroissante.
Soit Pn la propriété définie par:
pour tout

,

Initialisation: La propriété est-elle vraie au rang 2 ?
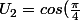 = \sqrt{2}/2)
donc

Soit h un entier tel que

, on suppose Ph vraie :

 \geq 0)
puisque
 \geq 0)
D'où

Pn est vraie au rang 2, elle est héréditaire, elle est donc vraie pour tout

)
est srtictement décroissante et minorée, donc elle converge.
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 18 Avr 2006, 17:34
par Mikou » 18 Avr 2006, 17:34
c'est juste mais la ligne 'donc
 0)
En effet soit une suite Un definie par U0 et U(n+1) = aUn, ou a <1, peut(on conclure que Un est decroissante ? non par exemple U0=3 et a = -0,5!
Il te reste plus qua traiter la seconde partie du probleme :happy2:
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 18 Avr 2006, 18:34
par Alpha » 18 Avr 2006, 18:34
Salut,
Personnellement, je suis assez tenté d'écrire
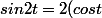 (sin t))
d'où
 = (sin 2t)/2(sin t))
.
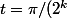)
pour

donne en remplaçant dans l'expression ci-dessus
 =)
...
et le télésopage dans le produit donne une expression très simple qui fournit immédiatement la convergence et la limite, sauf erreur (je n'ai rien écrit sur papier).
Cordialement
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 18 Avr 2006, 19:49
par Mikou » 18 Avr 2006, 19:49
alpha c'est astucieu si cela fonction , meme en donnant la forme explicite de Un avec lexercice que je propose la limite n'est pas evidente on tombe sur une forme indeterminée, toi et moi savons comment resoudre cela facilement, chut laisse chercher les autres :happy3:
Dailleurs si tu es interessé jai posté le sujet darithemetique du cg 2006, sais tu qui a participé sur le forum ? En tout cas pas moi pour une bien sombre raison ...
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 18 Avr 2006, 20:27
par Alpha » 18 Avr 2006, 20:27
Salut, la forme indéteminée est évidente, elle est connue depuis la 1ère! Enfin, c'est vrai qu'il faut penser à diviser et à multiplier par la bonne quantité, mais bon... C'est archi classique quand même!
Sinon pour le concours général je veux pas dire de bêtise mais je crois que Nightmare y a participé.
A+
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Avr 2006, 20:40
par Nightmare » 18 Avr 2006, 20:40
Bonsoir
Eh non, le concour général c'est niveau terminal, je n'ai participé qu'aux olympiades de 1ére.
:happy3:
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 19 Avr 2006, 06:45
par Mikou » 19 Avr 2006, 06:45
ha nightmare l'an prochin .... Sinon alpha je ne vois pas de quoi tu veux parler :hum:
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 19 Avr 2006, 07:37
par Alpha » 19 Avr 2006, 07:37
Oui c'est vrai Nightmare, j'ai confondu les deux! Désolé!
Sacré Mikou, tu ne vois pas ce dont je parle :ptdr: c'est bon ne fait pas la tête j'ai pas donné tant d'indications que ça...
A+
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 19 Avr 2006, 12:37
par Mikou » 19 Avr 2006, 12:37
oui c'est vrai peu de terminal connaissent le nom de telescopage meme si ils lutilisent souvent :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
