(niveau lycée?) Equation pour télécharger le plus vite

[Obouil]

Bonjour à tous,

Quand je télécharge sur internet ou même quand je transfère des fichiers, une question revient toujours :
Comment faire en sorte que le transfert soit le plus rapide ?

Par exemple j'ai 20 vidéos Youtube de 300 Mo chacune à télécharger avec un débit de 550 Ko/s.
Ou bien j'ai 20 dossiers de 2Go chacun situés dans des emplacement différents d'un disque, à transférer sur un autre disque en USB 2.0.
Je me retrouve souvent avec X nombre de dossiers ou fichiers à transférer.
Un certain débit de transfert (variable suivant la connexion internet ou USB).

Pour obtenir la durée de téléchargement la plus courte :
Faut-il lancer tous les téléchargement en même temps ? Ou bien faut-il les lancer un par un? Ou bien faut-il trouver la quantité idéale de données à transférer en bloc en fonction du débit ?

Si ce problème mathématique en intéresse certains, je serai ravi de vous lire.
En espérant avoir été clair dans mon énoncé.

[Sake]

Salut,

C'est plutôt élémentaire à première vue. La variable qu'il faut optimiser est le temps de transfert. Typiquement, nous nous appuyons sur un problème où le flux est le débit de chargement qui correspond à une quantité de données divisée par un temps. Ce débit est constant dans le temps et on peut le partager entre plusieurs fichiers (conservation du débit).

Ce débit Q se conservant, si on doit télécharger N fichiers pesant X octets chacun, il est clair que le débit de chargement d'un fichier est divisé par N pour chaque fichier. Le temps de téléchargement de chaque fichier sera de X/(Q/N) = NX/Q si on les lance tous en même temps. Comme ces téléchargements finiront tous en même temps, il s'agit aussi du temps complet de téléchargement.
Si on les lance séparément, le temps de téléchargement d'un fichier étant de X/Q, le temps de téléchargement des N fichiers est de NX/Q.

Il est donc indifférent de télécharger N fichiers à la suite des autres ou lancer les téléchargements simultanément. Bien-sûr, ce n'est plus vrai si le débit de téléchargement ne se conserve pas.
Quid de son évolution dans le temps ?

Supposons que le débit est une fonction de la variable temporelle t : Q = Q(t). Le temps de téléchargement est égal à où satisfait à l'équation : , les 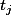satisfaisant à

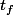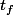Maintenant, le temps de téléchargement des N fichiers en même temps vaut où satisfait à l'équation : .

Puisque vaut 0, nous nous apercevons que et 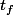satisfont tous deux à l'équation . Autrement dit, par monotonie de l'intégrale.

[Razes]

Ceci peut être différents dans le cas où la ligne autorise un certain débit et que tu télécharge des fichiers de plusieurs serveurs qui ont des débits différents 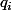et que les fichiers ont des tailles avec l'indice du serveur et l'indice du fichier ou des fichiers à télécharger du serveur indice .

[Obouil]

Merci beaucoup pour vos deux réponses.
Oui c'est vrai c'était assez élémentaire en fait... dans la pratique on n'a pas intuitivement cette impression.
Ca me rassure, bravo à vous deux et bonne continuation au forum.

[CitizenGui]

Salut,

Après si on reste sur la théorie, effectivement, à débit constant, que l'on charge tous les fichiers en un bloc ou un par un, ça ne change rien.
Dans la pratique, il faudrait prendre en compte la taille du fichier car il existe un temps incompréssible de l'écriture d'un fichier sur le disque ou de l'ouverture du flux pour le chargement.

Ainsi de 0 à n octets, un fichier mettra toujours x secondes pour arriver.
L'optimisation serait alors de traiter les petits fichiers en parallèle d'un gros.

Edit: Et puis on peut aussi complexifier en ajoutant un buffer de m octets qui limiterai l'effet de l'écriture.