Netflix_maths saison 2

[beagle]

"Ceux qui veulent continuer à s'amuser peuvent lire et/ou participer, tout le monde sait bien qu'on y va pour lire des bouffoneries. "
"J'ai donc résolu l'exercice et cela sans même comprendre "

oui bouffonne

Bien sur que l'on utilise un élément connu de la série pour choisir.
Tout le monde le sait, je l'ai meme appelé un critère de sélection.
Bon on a vu que depuis le début de ce fil tu me prends pour un con, et tu fais ton cinéma juste pour pourrir le fil de discussion. C'était visible, tu crois que je ne le savais pas ?

Vas-y , ça tourne, un prof de maths qui enseigne proba stats au supérieur, ne sait pas ce que c'est gagner en jouant le retard d'une série:
vas-y : MOTEUR !

[Vassillia]

Comme on ne peut pas gagner plus souvent qu'au hasard en jouant le retard d'une série, non effectivement je ne sais pas, tu peux mettre tout ce que tu veux derrière, peu m'importe.

Mais je suis pas si mauvaise en pédagogie, la preuve, tu as effectivement compris l'image que j'ai de toi sans que j'ai eu à le dire

[beagle]

Comme on ne peut pas gagner plus souvent qu'au hasard en jouant le retard d'une série, non effectivement je ne sais pas, tu peux mettre tout ce que tu veux derrière, peu m'importe.

Bon alors finalement tu n'as rien compris en fait.
On joue le retard sur des séries dont on connait un critère,
ce qui change tout.

[Vassillia]

Mais si j'ai compris sauf que l'on peut mettre jouer le retard, avoir un premier tirage qui donne pile, avoir un dernier tirage qui donne face... n'importe quoi d'autre je m'en fiche.

Tant que j'ai une information meme partielle sur la survenue de cet événement et que je peux choisir uniquement les series qui m'arrangent, évidemment que je peux créer artificiellement une probabilité conditionnelle supérieure à 50%.

[beagle]

Mais si j'ai compris sauf que l'on peut mettre jouer le retard, avoir un premier tirage qui donne pile, avoir un dernier tirage qui donne face... n'importe quoi d'autre je m'en fiche.

Tant que j'ai une information meme partielle sur la survenue de cet événement et que je peux choisir uniquement les series qui m'arrangent, évidemment que je peux créer artificiellement une probabilité conditionnelle supérieure à 50%.

ben c'est ce qu'on te demande,
une proposition de critère et ensuite des probas intéressantes différentes de 50%
Le but n'est pas forcément d'avoir la tatctique max,
mais déjà des trucs qui se rapproche de sur 25% des series on gagne plus de 95% des fois
sur la moitié des séries on gagne je crois plus de 80%

sors nous un critère et des résultats un peu.

[lyceen95]

Je ne sais toujours pas où tu veux en venir.
Cette discussion :
- C'est une question ? Tu demandes de l'aide sur un sujet ?
- C'est une énigme ? Tu as un sujet amusant et tu défies les gens de trouver la solution ?
- C'est une information ?
A priori, la discussion n'entre dans aucune de ces 3 cases.
C'est donc la 4ème option : tu trolles , tu cherches à pourrir ce forum avec des discussions qui n'ont aucun sens.

Ou une 5ème option : tu es devenu idiot.

Dans les différents cas, tu connais l'adresse d'un forum adapté pour ces discussions trollesques ... inutile que je te la rappelle.

[Vassillia]

Dans des conditions normales de discussion, cela aurait peut-être pu m'amuser mais les conditions ne sont pas normales et j'en ai plus que marre de ton attitude envers moi.
Pourquoi je continuerai à m’intéresser à ton exercice ? Tu crois vraiment que j'ai quelque chose à prouver, si je participe, c'est pour me faire plaisir et pour faire plaisir à ceux avec qui j'échange et je ne prends aucun plaisir vu le contexte.
Désolée mais j'ai vraiment essayé de répondre sérieusement au départ sauf que la joute oratoire est systématique et je sais que même si je réponds sérieusement cela va continuer encore et encore.

Si certains lecteurs en ont envie, parceque eux je les respecte, je traduis de sorte à ce que Beagle puisse corriger si besoin :
Soit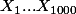 une suite de variables iid suivant une loi de Bernoulli

On joue le retard, à savoir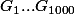 une suite de variables définies tel que :
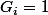si la valeur obtenue avec va dans le sens de rattraper le retard
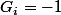si la valeur obtenue avec va dans le sens d'augmenter le retard
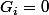si pas de retard à l'étape 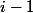(enfin à confirmer auprès de Beagle, il n'a pas encore précisé)
Le gain final est

On cherche un critère, à savoir une fonction et un réel tels que : (enfin j'imagine qu'on peut aussi avoir une égalité comme c'est un problème ouvert).

La question 1) est de trouver un critère pour avoir une probabilité conditionnelle de gain supérieure à 50% autrement dit
Tant qu'à faire on regardera la probabilité de vérifier ce critère autrement dit

Pour la question 2) on a une permutation aléatoire avant de calculer le gain mais après l'avoir choisi grâce au critère. Autrement dit si est la permutation, on veut regarder l'évolution de

PS : mon critère est de prendre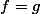 et 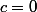donc je trouve une probabilité conditionnelle de 100% mais je suis d'accord que l'exercice peut être plus intéressant que cela

[beagle]

"Pourquoi je continuerai à m’intéresser à ton exercice ? Tu crois vraiment que j'ai quelque chose à prouver, si je participe, c'est pour me faire plaisir et pour faire plaisir à ceux avec qui j'échange et je ne prends aucun plaisir vu le contexte. "

non ton plaisir depuis le début est de jouer en contre.
C'est toi qui sur un exercec ouvert me demande redemande de valider.
Ben non rien à valider tu fais si tu as envie sur les pistes de tes envies…

Ensuite apres avoir passé ton temps à dire que c'est pas défini que l'on ne comprend rien,
par deux fois tu appelles cela des bouffonneries …
Ton plaisir depuis le début n'est pas dans ce à quoi on joue, ni où on peut aller, mais juste démolir.
c'est réussi d'ailleurs.

Donc on s'en tape de ta réécriture mathématique qui enferme l'exo,
critère de selection et mode de démonstration du retard sont des propositions ouvertes.

[Vassillia]

@Beagle, je n'ai pas été assez claire visiblement, je ne l'ai pas réécrit pour toi mais pour les lecteurs qui voulaient comprendre, un fil à partir du moment où il est public ne t'appartient pas que je sache

[beagle]

oui et bien ton écriture ne rend pas compte des cas possibles, alors tu devrais moins frimer à faire celle qui a bien défini le retard et comment on l'analyse.
Il y a quantité de façons de faire, et tout le monde comprend ce qu'est le retard et gagner quand on joue le retard, apres quel retard où quand comment laisse donc faire ou va ouvrir un autre fil de discussion avec tes propres critères.

[Vassillia]

C'est bien pour cela que j'avais proposé d'autres hypothèses pour le retard, lire les messages précédents.
Je me suis contentée de prendre la dernière que tu as donné, celle de LeJeu que j'ai répété à chaque tirage mais j'avais proposé précédemment de ne le faire que sur le dernier tirage.
Si tu veux que je n’intervienne pas, tu sais où poster car ici je te préviens, je le ferai systématiquement

[lyceen95]

J'aimerais comprendre ... mais c'est compliqué.

Voici où j'en suis :
Il y a un type qui lance une pièce ... et qui répète cette opération régulièrement. Une pièce non truquée, classique.
Il y a un joueur qui parie sur le résultat de ce lancer.
Juste avant chaque lancer, le joueur parie.
La question est : le joueur aurait-t-il un quelconque avantage à parier sur le retard, autrement dit à parier sur le côté qui est apparu le moins souvent lors des derniers lancers .
C'est ça la question ?

J'ai vu passer des tas de discussions sur le sujet. J'ai vu un forumeur au pseudo Beagle dire à différentes reprises que les lancers étant indépendants, le joueur 'avisé' n'avait aucun avantage sur le joueur non avisé.
J'ai vu des manipulateurs sortir des théories totalement fumeuses pour défendre l'indéfendable, des gens d'une telle mauvaise foi qu'ils se sont fait exclure de tous les forums ayant un minimum de déonthologie.

Là dessus, tout le monde est clair, y compris le Beagle d'il y a un an, le joueur avisé n'a aucun avantage sur le joueur non avisé.

Il n'y a pas de débat .

Le Beagle d'aujourd'hui est-il en train de renier le Beagle des années passées.
C'est ça le sujet ?

[beagle]

lycéen la série est terminée et j'ai UNE info .
Si vous laissiez évoluer les fils de discussion on serait rendu à l'évidence et au pourquoi comment ça marche,
mais avec vous ça pinaille dès le début,
donc on n'avance jamais là où c'est intéressant.

[azf]

Pardon Lycéen mais tout le monde est d'accord (même Beagle et si j'ai bien compris ce sujet)

Il n'y a aucun avantage particulier à détenir des informations sur le passé : chaque lancé possède 1 chance sur deux de tomber sur pile (c'est le hasard en tant que tel sans mémoire du passé)

Quand bien même auparavant on a eut 10000000000000000000000000000000^nombre de Graham de faces sortie d'affilées

Par contre je ne comprend toujours pas l'intérêt de retenir des critères pour jouer "au retard"

[Vassillia]

@Lyceen95 En gros la question est de trouver P(gain au retard|info sur la serie). Comme c'est ouvert et qu'on peut mettre ce qu'on veut derrière les mots je choisis "info sur la série" = "gain au retard"
Voilà comment obtenir une jolie proba qui vaut 100% et je t'assure que je ne plaisante même pas. C'est vraiment de cela qu'il est question.

@azf En l'état aucun intérêt pour moi mais si on précise ce qu'il y a derrière "gain au retard" et derrière "info sur la serie" on peut faire un exercice amusant comme les variables aleatoires correspondantes ne sont pas indépendantes.

[azf]

C'est moi ou j'ai rien compris?
Pardon mais une série telle que donnée dans l'énoncé ne possède aucune info
Les tirages qui composent une série sont indépendants des uns des autres
On peut très bien avoir une série de 10^10 piles d'affilés et n'empêche qu'au coup suivant on aura une chance sur deux d'avoir un pile et se retrouver facilement (une chance sur deux d'avoir réalisé (10^10)+1 piles

[beagle]

azf je vais tout mettre sur le site de Pierre,
vu le niveau dans lequel veut nous entrainer Vassillia.

C'est à la fois trivial et intéressant si on veut discuter…
mais nous sommes en page 3 et rien n'a démarré, alors ...

[Vassillia]

@azf tu as raison, en pratique on n'aura jamais aucune info mais c'est juste un exercice de pensée. On essaye de jouer au loto en devinant des boules déjà sorties, j'ai confiance en nous, on va gagner.

[lyceen95]

La série est terminée et j'ai UNE info.
Si tu ne dis pas la nature de cette info, ne t'étonne pas qu'on tourne en rond.

Personnellement, je ne sais toujours pas de quoi tu veux parler.
On est page 3, et tu n'as toujours rien dit de vraiment CLAIR.

[azf]

@azf tu as raison, en pratique on n'aura jamais aucune info mais c'est juste un exercice de pensée.

ok et donc on doit montrer que toute information sur toute série possède la même "valeur" et que celle-ci est nulle (genre l'info qui dit que les trains arrivent à l'heure)

c'est ça ?