Moins de n serpents

[Imod]

Bonjour

Une question venue d'ailleurs qui devrait intéresser plusieurs intervenants du site ( je n'illustre pas car je ne comprends plus rien à l'insertion d'images ) .

On remplit une grille carrée nXn avec des serpents se déplaçant vers la droite , du genre montants ou descendants . Par exemple : HHDDHDHH ou DBBBDBDB . Il y a des serpents hybrides : HHH , DDD ou encore D , H , qui n'entrent dans aucune catégorie mais ils sont acceptés .

Pourquoi ne peut-on pas remplir la grille avec moins de n de ces serpents ?

Imod

[Pseuda]

Une idée (je ne sais pas si ça sert). Pour remplir la grille nxn avec un seul serpent, il doit passer au moins N "coudes" (N à déterminer). Chaque serpent peut produire un seul coude au maximum. Il faut donc couper le serpent, et il faudrait aboutir en, au minimum n tronçons.
Le seul problème, c'est qu'on peut remplir la grille avec des tronçons qui n'en formeraient pas un seul, même si on les reliait.

La récurrence me paraît difficile.

[Ben314]

Salut,
J'ai peut-être un début d'idée, mais je suis pas sûr à 100% que ça marche (et c'est pas très joli...)
- Si tout serpent sont de longueur <= n, le résultat est évident.
- S'il y a un serpent de longueur > n, j'ai l'impression que, dans ce qui n'est pas recouvert par ce serpent, on peut trouver deux carrés de taille respectives PxP et QxQ avec P+Q=N-1 et tels qu'ils soit impossible à un quelconque serpent d'aller de l'un à l'autre (en restant dans la zone non recouverte par le premier serpent).
Sauf erreur, ça constituerais une preuve (par récurrence), mais autant je suis (quasi) certain de l'existence des deux carrés, autant je suis pas certain du tout du fait qu'il n'y a pas de serpent allant de l'un à l'autre.

[beagle]

modifié 28 mars

[Pseuda]

J'affine un peu avec les "coudes". Il faut passer 2(n-1) coudes avec un seul serpent pour une grille nxn. Chaque petit serpent peut passer un coude au maximum. Quand on coupe le serpent unique du départ, au bon endroit (à l'endroit d'un coude), on évite un coude et on crée 1 serpent supplémentaire.

Je ne sais pas si cela peut aboutir, il y a des zones d'ombre.

[Imod]

Bonjour à tous :

@Pseuda : un serpent peut avoir plusieurs coudes .
@Ben : en effet les deux carrés peuvent à priori partager un serpent donc le raisonnement n'est pas complet .
@Beagle : si un serpent traverse de bord à bord le problème est réglé avec l'argument de Ben mais ce n'est malheureusement pas toujours le cas .

Le problème n'est pas simple

Imod

[Pseuda]

@Pseuda : un serpent peut avoir plusieurs coudes .

Le problème n'est pas simple

Ouais j'ai lu trop vite. Oui, il ne se résout pas en 5 minutes.

[Imod]

Je précise que j'ai deux solutions (quasi sûres ) à l'énigme : celle de l'auteur et la mienne . Les deux méthodes sont extrêmement différentes alors je ne donne aucun indice dans l'espoir de voir apparaitre une nouvelle approche plus simple .

Il m'a fallu deux semaines pour trouver l'idée de la solution , alors pas de précipitation et osez essayer dans tous les sens .

Imod

[beagle]

modifié le 28 mars

[nodgim]

"Dominique t'est pénible d'avoir fait cela."

C'est en effet une énigme que je qualifie assassine. De celle qui vous prend la tête un bon moment sans pour autant avoir l'assurance de pouvoir la résoudre un jour.

[Pseuda]

En fait, sans le vouloir, je me suis attaquée à une autre énigme, beaucoup plus facile, qu'une grille nxn se remplit avec au minimum n serpents qui ne peuvent avoir qu'un coude au maximum (HD, DH, BD ou DB). C'est curieux comme on aboutit au même résultat (je pense que c'est vrai, mais pas le temps d'approfondir). Cela ne se résout apparemment pas de la même façon.

[Ben314]

Peut-être une piste :

Clairement le plus grand serpent qui rentre, il a une longueur de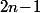 et il y en a au plus un de cette longueur. Ensuite, s'il y en a un de longueur 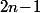alors il n'y a en pas de longueur 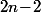et s'il n'y en a pas de longueur 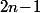alors il n'y a au plus 2 de longueur .
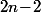Bref, si on note le nombre de serpent de longueur , alors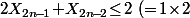
Ensuite, en regardant la façon de placer des "gros" serpents, j'ai l'impression que
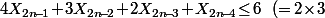puis que
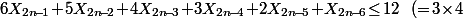etc... et donc qu'au final

Or on a évidement
Et en soustrayant les équations on obtient .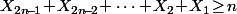

Bon, évidement, ça avance pas à grand chose vu que la dernière inégalité est totalement équivalente à celle qu'on doit démontrer (donc faut démontrer des trucs en plus de ce qui est demandé).
Mais ça donne des "bouts de piste" vu que la première inégalité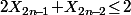 se voit "assez bien" sur un dessin et qu'il faudrait comprendre comment en faire une preuve "pur calcul" pour pouvoir l'adapter aux inégalités suivantes.

[Archytas]

Je n'ai pas compris quelque chose : par chaque case du carré n x n passe exactement un serpent ou plusieurs sont autorisés ?

[Ben314]

Selon moi, les différents serpents recouvrent la grille, ou forment une partition si tu préfère.
Mais d'un autre coté, je me demande si ça ne continue pas à être vrai si on accepte que les serpents se chevauchent (sur de petits carrés, ça semble marcher aussi...) et, si c'est le cas, c'est peut être (???) plus facile à montrer vu qu'il n'y a plus de problème de connexité.
(par contre mon truc du post précédent, c'est complètement faux si on accepte que ça chevauche).

EDIT (après coup...) : non, si on accepte que ça se chevauche, ça marche plus : on peut recouvrir un 4x4 avec seulement 3 serpents.

[Imod]

Oui les serpents sont disjoints . Le problème de Pseuda est intéressant aussi avec des serpents ayant chacun un angle au maximum : il est certainement plus simple .

Une autre inégalité dans le style de celle de Ben mais je ne l'ai pas montrée : la somme des cases occupées par serpents sur une grille 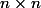est majorée par .

Imod

[Pseuda]

Bonjour,

Une autre idée (je n'ai pas trop de temps, mais bon, quand tu nous tiens), cette fois pour le bon problème.

J'ai l'impression qu'on pourrait généraliser le problème à n'importe quel quadrillage convexe (par exemple en forme de pyramide, ...) de petits carrés juxtaposés par au moins un côté (par un coin : interdit). Et que pour remplir ce quadrillage, il y a un nombre minimum de serpents pour le remplir, associé à ce quadrillage.

Ce qui va compter pour remplir le quadrillage, c'est le nombre de bords, et le nombre de figures d'un carré 2x2 compris dedans. Chacune de ces figures a un centre. Appelons-les des "centres" (centre du carré 2x2). Par exemple, pour une pyramide 5-3-1 carrés, il faut un serpent pour chaque bord (soit 2 serpents) + 2 serpents (1 pour chaque "centre") - 1 (car les 2 centres sont juxtaposés), soit 3 serpents.

Pour un carré nxn, il y a 2 bords (en L, un de chaque côté), puis (n-1)^2 centres à l'intérieur contigus. On recommence, dans ce carré (n-2)^2, il y a 2 bords, puis (n-3)^2 centres à l'intérieur. Etc.... Jusqu'à :
- 0 carré si n est pair : le nombre de serpents = 2 * somme des pairs jusqu'à n = n serpents
- 1 carré si n est impair : le nombre de serpents = 1 + 2 * somme des impairs jusqu'à n = n serpents aussi.
Ceci constitue un minimum de serpents pour le remplir.

Ce n'est qu'une idée. Il reste à mettre tout cela d'aplomb pour justifier rigoureusement, c'est la 2ème étape (la plus difficile ?), si tant est que cette approche tient la route.

[Imod]

Attention le problème est hyper-addictif , personnellement j'ai réussi à l'oublier pendant une semaine et la solution est apparue miraculeusement quand j'ai regardé ça :

[Image jointe refusée]

Imod

[Pseuda]

@Imod, l'image a été refusée.

[Imod]

Je sais , le site propose de joindre des images directement ou d'ajouter un lien vers certains hébergeurs d'images . Il y a quelque temps , seule la deuxième solution était possible et elle rend illisible des tas de sujets intéressants . J'attends de savoir si on peut réellement joindre une image sur ce site sans dépendre du bon vouloir d'intervenants extérieurs .

Désolé de lancer une polémique sur un problème qui mérite bien mieux

Imod

[Archytas]

Selon moi, les différents serpents recouvrent la grille, ou forment une partition si tu préfère.

Ok je comprends ! Pour moi un recouvrement, au contraire, ne demande pas la disjonction (recouvrement ouvert d'un espace topologique). Mais très bien, j'essaierai de gratouiller quelques trucs quand j'aurai l'occasion, le problème est effectivement sympa !