Minimum : le retour !

[Chimerade]

Dans la suite de http://www.maths-forum.com/showthread.php?t=4612, où j'ai posé un problème apparemment bien connu et où Galt et d'autres ont donné des réponses intéressantes, je voudrais corser un peu le problème :

Comment trouver le point M qui minimise la somme 4 MA+ 5 MB+ 6 MC, A, B, C étant trois points donnés ! Et le point P qui minimise la somme !

Les points A, B et C étant tracés sur une feuille, construire ces points à l'aide d'un double décimètre, de la règle et du compas !

[Mikou]

:) dailleurs personne n'a donné de reponse complete au precedent pb, no n ?

[yos]

On calcule le gradient de f : M--->4MA+5MB+6MC.
Le gradient de M--->MA est .
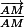
Celui de f est donc .
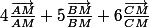
Ce gradient est nul au(x) point(s) cherché(s). (Il est clair que f n'a pas de maximum).

Je vous laisse trouver un moyen de construire un tel point M s'il en existe.

A noter qu'avec MA+MB+MC, c'est facile car alors il faut trois vecteurs unitaires de somme nulle "partant" de M, ce qui ne peut se faire qu'avec des angles de 120° entre eux. C'est infaisable si le triangle a un angle >120° (auquel cas le min est en ce sommet). Et sinon on retrouve le point de Fermat, intersection des droites (AA'),(BB'),(CC') où BCA' est équilatéral extérieur à ABC ...