Max dans triangle

[yos]

Bon voilà deux sujets de réflexion pas trop durs avant que je parte en vacances :
1)Quels sont les triangles dont la somme des cosinus des angles est maximum?
2)Quels sont les triangles dont le rapport est maximum?
Bon courage.

[nekros]

humm j'y réfléchirai demain ...

[aviateurpilot]

j'ai trouver que
donc
car peut etre egal à
par exemple pour

[nekros]

Oui tu as tout à fait raison.
Il reste à trouver A,B et C.

Voilà ce que je propose :

Notons , et ces trois angles

On a : soit encore

Or, et

On a donc :

Posons et

On a donc

On résout en et on trouve que la seule solution est et par conséquent,

Il reste à remplacer et on trouve que , c'est-à-dire que le triangle est équilatéral.

Thomas G :zen:

[aviateurpilot]

1)
puisque la fonction cos est concave.
=> si on prend A,B,C de

avec egalite si et seulement si
triangle equilateral
=> sinon, on prend A et B de et


les triangles dont la somme des cosinus des angles est maximum sont les triangle equilateral
pour 2)
dsl car je ne connais pas des formule sur r et R

[nekros]

aviateurpilot,

Pour le 2, le rayon du cercle inscrit est donné par avec S la surface du triangle.

De plus, son centre est le barycentre des points pondérés ,, et

D'autre part le rayon du cercle circonscrit au triangle implique qu'il soit rectangle et on a :

On a donc

Thomas G :zen:

[buzard]

D'autre part le rayon du cercle circonscrit au triangle implique qu'il soit rectangle

c'est jolie ca, on connais pas la formule générale, alors on simplifie le probleme! Depuis quand les triangles sont-il tous rectangle.

pour le 2), à l'aide de maple on trouve le triangle equilateral aussi, ca parait logique c'est celui qui remplit le plus son cercle circonscrit.


Ma methode certe bourine mais qui fonctionne, est d'exprimer toutes les coordonnées en fonction de :



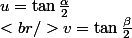
Ah oui j'oubliais, j'utilise une repère bipolaire avec le coté AB=1 (car le rapport lambda est le meme pour des triangles semblables). On se limite également aux triangles sans angle optu en A ou en B, car dans un triangle il ne peut y avoir qu'un seul angle obtu (autant qu'il soit en C).
d'où , ce qui revient à , avec le changement de variable.

on arrive finallement à l'aide de maple, à
qui s'avère possèder un maximum en
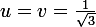
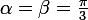
qui correspond à c'est à dire au triangle équilatéral. Je laisse les détails sordide du calcul à maple, il le fait bien.

[buzard]

on arrive finallement à l'aide de maple, à

On peut rendre la formule symetrique en $\alpha$, $\beta$ et $\gamma$, ce qui parait plus logique.

et d'autre part:

donc finalement :

ou encore si on veut revenir aux u v et w :

on peut utiliser sans probleme les racine car les angles moitié sont tous inférieur à pi/2 donc les sin cos et tan sont bien positifs.

autr remarque : si on note alors on a