Matrices diagonalisables

[Nightmare]

Puisque l'heure semble être à l'algèbre linéaire :

Montrer que l'ensemble des matrices diagonalisables de est dense dans ce dernier. Quel est son intérieur?

[Joker62]

Haileau.

En trigonalisant et en modifiant la base pour que les termes au dessus la diagonales soient tous inférieur à un certain epsilon on peut construire une suite de matrice qui tendent vers la matrice de départ.

Contre-exemple dans Mn(R) ? Belle application de la continuïté du discriminant :)

[Ben314]

Et, sauf erreur, l'intérieur est l'ensemble des matrices diagonalisables à valeur propres 2 à 2 distinctes.
On peut le voir en montrant que l'application qui à une matrice associe son polynôme caractéristique est continue (ce qui permet aussi de voir pourquoi les matrices diagonalisables sont denses)

[Joker62]

Y'a pas une application avec les résultants ? Je me rappelle plus trop...

[Matt_01]

Je dirais que pour une matrice triangulaire supérieure de diagonale avec tous les 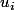distincts, on peut procéder ainsi :
On considère la matrice triangulaire supérieure égale à la première, si ce n'est sur la diagonale ou elle vaut où les sont choisis de telle sorte que tous les termes soient distincts. En faisant tendre vers (on prend une sous suite gardant les termes tous distincts, cela étant possible car l'égalité sur une partie infinie de R (ie une boule centrée en 0) donne l'égalité des polynômes en obtenus, ce qui est impossible), on obtient ce qu'on veut (la matrice est diagonalisable en considéront son polynôme caractéristique).

Après en utilisant que toute matrice complexe est trigonalisable, on conclut. Je réflechis à l'intérieur.

[Matt_01]

Puis en fait comme l'ensemble des matrices diagonalisables à vap deux à deux distincts est ouvert (d'après la continuité de la fonction qui à une matrice associe son polynôme caractéristique), et que son adhérence est l'ensemble des matrices, on peut déduire l'intérieur des matrices diagonalisables.

[benekire2]

Salut !

Il faut quoi comme prérequis ? J'ai l'impression au vu de l'énoncé et des réponses qu'il faut avoir fait de la topologie et de la réduction et évidemment je connais rien de tout ça .

[Matt_01]

Oui c'est ça topologie et réduction :)

[windows7]

salut,

interieur : le poly. caracteristique est scindé simplement.

comme le suggere Joker on regarde via une methode de perturbation.

[Nightmare]

Il ne vous aura pas tenu en haleine très longtemps :happy3:

[Joker62]

J'ai retrouvé une application agréable :

On montre avec ça que C[u] = Commutant(u) => u est cyclique
Où C[u] c'est l'ensemble des polynôme en u

[Nightmare]

Joker62 > Tiens, comment ferais-tu pour montrer ça au contraire sans utiliser ce qu'on vient de faire ?

[Joker62]

Le résultat cité utilise aussi la semi-continuité inférieure de l'application rang
Donc sans ce résultat on part d'une technique sur la dimension.

On montre que la dimension du commutant est toujours supérieure à n
On utilise la réduction de Frobenius de A que l'on note B
On a donc l'existence d'une matrice inversible P telle que A = PBP^-1 (par construction)

On déduit par un isomorphisme entre Comm(A) et Comm(B) (C =---> P^-1 C P) que les dim de Comm(A) et Comm(B) sont égales

On peut donc se ramener à travailler avec des blocs compagnons (Etape un peu plus délicate)

Et on s'en sort en disant que pour les matrices cyclique, polynôme caractéristique et polynôme minimal sont les mêmes.

Comme la famille {I,A,A^2,...} est de rang n, on a dim comm(A) >= n

C'est un truc dans le genre, y'a des étapes pas trop claires.
Ca se trouve dans le Gourdon et dans le Francinou,

Sinon l'autre vient de Cognet qui est plus intéressant.