Bonjour,
J'ai trouvé cet exercice sur internet, je n'ai pas encore réféchis a comment le faire, mais parait-il c'est quelque chose de "connu" alors je le poste ici pour que tout le monde puisse en profiter.
Montrer que toute matrice tridiagonale de diagonale nulle de taille 2k+1 pour k entier est de déterminant nul.
Bon travail :id:
(J'espère au moins que ce n'est pas bidon :ptdr: )
Matrice tridiagonale
5 messages
- Page 1 sur 1
Pour le déterminant d'une matrice tridiagonale on a toujours un lien de récurrence entre le déterminant à l'ordre n et celui aux ordres  et
et 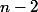 (on le voit en développant par rapport à la dernière ligne). Ici, si je note
(on le voit en développant par rapport à la dernière ligne). Ici, si je note  les éléments de la sur-diagonale et
les éléments de la sur-diagonale et  ceux de la sous-diagonale, et
ceux de la sous-diagonale, et 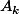 la matrice d'ordre
la matrice d'ordre 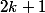 que l'on considère on obtient que
que l'on considère on obtient que 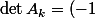^{2k+1+2k}b_{2k}a_{2k}\det A_{k-1}) donc il suffit de vérifier la propriété pour les matrices tridiagonales à diagonale nulle d'ordre
donc il suffit de vérifier la propriété pour les matrices tridiagonales à diagonale nulle d'ordre  ce qui est immédiat.
ce qui est immédiat.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
