Limite...
Olympiades mathématiques, énigmes et défis
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 18 Nov 2006, 16:29
par bitonio » 18 Nov 2006, 16:29
Bonjour,
voila un exo posé par notre prof de sup. Je le trouve assez interessant

calculer
^{1 \over x})
Bonne chance!
Ciao
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Nov 2006, 17:13
par Nightmare » 18 Nov 2006, 17:13
Bonjour
Sans mettre la démo je trouve que la limite vaut ln(a) si b < a et vaut +oo si b > a
:happy3:
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 18 Nov 2006, 17:18
par bitonio » 18 Nov 2006, 17:18
Raté :we: De toute facon comme le choix et a et b est arbitraire, ton raisonement ne peut pas tenir la route
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Nov 2006, 17:25
par Nightmare » 18 Nov 2006, 17:25
Oups, oubli d'un facteur.
Nouvelle réponse :
ln(a) si b < a et ln(a)+ln(b/a) si a < b
:happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Nov 2006, 17:32
par Nightmare » 18 Nov 2006, 17:32
Mon raisonnement.
=\(\frac{a^{x}+b^{x}}{2}\)^{\frac{1}{x}})
)=\frac{1}{x}ln\(\frac{a^{x}(1+\(\frac{b}{a}\)^{x}}{2}\))
)=\frac{1}{x}ln(a^{x}}+\frac{1}{x}ln(1+\(\frac{b}{a}\)^{x})-\frac{ln(2)}{x})
)=ln(a)-\frac{ln(2)}{x}+\frac{1}{x}ln(1+\(\frac{b}{a}\)^{x}))
Si b a ,
^{x})=ln(\(\frac{b}{a}\)^{x})+ln(1+\(\frac{a}{b}\)^{x}))
Finalement :
^{x})=ln\(\frac{b}{a}\)+\frac{1}{x}ln(1+\(\frac{a}{b}\)^{x})\longrightarrow_{x\to +\infty} ln\(\frac{b}{a}\))
Finalement
)\longrightarrow_{x\to +\infty} ln(a)+ln\(\frac{b}{a}\))
d'où f converge vers b
:happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Nov 2006, 17:32
par Nightmare » 18 Nov 2006, 17:32
Bon, modulo le LaTeX défaillant, on comprend
:happy3:
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 18 Nov 2006, 17:44
par bitonio » 18 Nov 2006, 17:44
Oui c'est la bonne réponse! c'est en effet max(a,b)! bravo :) Cependant il y a beaucoup plus simple avec des DL ...
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 03 Déc 2006, 02:27
par darkmaster » 03 Déc 2006, 02:27
j'ai une autre solution.
Si
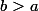
on a
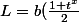^{\frac1x})
où
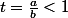

donc

et

Par suite,
^0=b)
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 03 Déc 2006, 02:55
par darkmaster » 03 Déc 2006, 02:55
Et je crois que la limite de
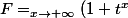^x)
où
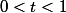
est plus difficile... :marteau:
-
steef91
- Membre Naturel
- Messages: 19
- Enregistré le: 25 Jan 2007, 21:00
-
 par steef91 » 19 Mai 2007, 15:20
par steef91 » 19 Mai 2007, 15:20
darkmaster a écrit:Et je crois que la limite de
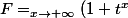^x)
où
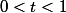
est plus difficile... :marteau:
je serrai curieux de savoir à quoi c'est égal

-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 19 Mai 2007, 15:25
par fahr451 » 19 Mai 2007, 15:25
steef91 a écrit:je serrai curieux de savoir à quoi c'est égal

on va dire 1 pour faire simple
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités