La ligne polygonale dans le carré
20 messages
- Page 1 sur 1
La ligne polygonale dans le carré
Bonjour,
Dans un carré de côté 1, on trace une ligne polygonale de longueur supérieure à 1000. Montrer qu'il existe un segment parallèle à un côté du carré qui rencontre la ligne en 500 points au moins.
Dans un carré de côté 1, on trace une ligne polygonale de longueur supérieure à 1000. Montrer qu'il existe un segment parallèle à un côté du carré qui rencontre la ligne en 500 points au moins.
Au tomber du lit , l'idée que j'avais eue hier semble tenir la route .
On note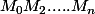 la ligne brisée de longueur supérieure à 1000 et contenue dans le carré de côté 1 . On muni le plan d'un repère orthonormé
la ligne brisée de longueur supérieure à 1000 et contenue dans le carré de côté 1 . On muni le plan d'un repère orthonormé ) avec
avec  ,
,  ,
,  trois coins consécutifs du carré . Les points
trois coins consécutifs du carré . Les points 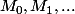 se projettent en
se projettent en 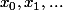 et
et 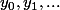 sur les axes de coordonnées .
sur les axes de coordonnées .
D'après l'inégalité triangulaire :
Notons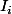 l'intervalle dont les extrémités sont
l'intervalle dont les extrémités sont  et
et 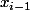 ,
, 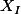 , la fonction caractéristique de l'intervalle
, la fonction caractéristique de l'intervalle  et
et 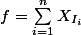 .
.
dt=\int_0^1 \sum_{i=1}^n X_{I_i}(t)dt=\sum_{i=1}^n \int_0^1X_{I_i}(t)dt= \sum_{i=1}^n |x_i-x_{i-1}| > 500})
Alors la fonction f prend des valeurs supérieures à 500 . Or>500) signifie que
signifie que  appartient à plus de 500 intervalles
appartient à plus de 500 intervalles 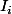 donc que la ligne brisée coupe la droite d'équation
donc que la ligne brisée coupe la droite d'équation 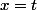 en plus de 500 points .
en plus de 500 points .
Imod
On note
D'après l'inégalité triangulaire :
Notons
Alors la fonction f prend des valeurs supérieures à 500 . Or
Imod
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
