Les tiroirs sont-ils assez grands ?
Olympiades mathématiques, énigmes et défis
-
Arbre
 par Arbre » 13 Jan 2017, 16:51
par Arbre » 13 Jan 2017, 16:51
Bonjour,
Je suis le conseil de Ben et ouvre 3 conversations une pour chaque énigme :
énoncé 5 : les tiroirs sont-ils assez grands ?Soit
_{n\in\N^*})
une suite d'entiers naturels non nul, majorée, tel que
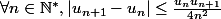
A-t-on alors, l'existence d'un point fixe pour la suite,
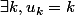
?
Bonne journée.
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 13 Jan 2017, 18:33
par L.A. » 13 Jan 2017, 18:33
Bonjour,
Supposons qu'une telle suite n'a pas de point fixe, alors au début on aura
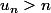
jusqu'à un premier rang

où
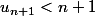
, car la suite est majorée. On a donc
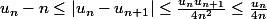
ce qui entraîne
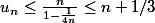
.
Or il n'existe aucun nombre entier compris entre n strictement et n+1/3, contradiction.

EDIT : désolé pour le spoil, je ne trouve pas le moyen de cacher les parties en tex...
-
Arbre
 par Arbre » 13 Jan 2017, 18:53
par Arbre » 13 Jan 2017, 18:53
Bonsoir,
Cela doit être tout con, mais je ne vois pas pourquoi :
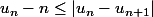
Bonne soirée.
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 13 Jan 2017, 18:57
par L.A. » 13 Jan 2017, 18:57
On a
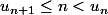
donc
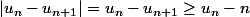
.
-
Arbre
 par Arbre » 13 Jan 2017, 19:39
par Arbre » 13 Jan 2017, 19:39
Ok.
Et enfin pour ces 2 inégalités :
L.A. a écrit: 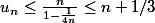
Comment les obtiens-tu ?
Merci et désolé pour ma lenteur d'esprit.
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 13 Jan 2017, 20:19
par L.A. » 13 Jan 2017, 20:19
A partir de
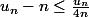
tu obtiens
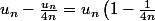 \leq n)
puis
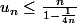
(car

entaîne
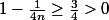
).
Enfin
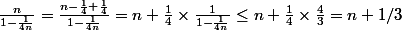

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Jan 2017, 20:23
par Ben314 » 13 Jan 2017, 20:23
Perso, j'aurais pas procédé par l'absurde (je sais pas qui se rappelle de Léon...),
mais ça ne change strictement rien aux calculs.
Comme
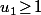
et que la suite
_{n\geq 1})
est majorée, c'est que
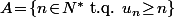
est non vide et majoré donc admet un plus grand élément

.
On a donc
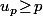
et
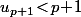
c'est à dire en fait
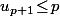
et on en déduit que
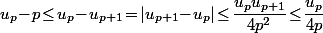
c'est à dire
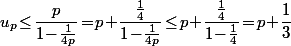
donc
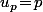
.
Modifié en dernier par
Ben314 le 14 Jan 2017, 04:20, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Arbre
 par Arbre » 13 Jan 2017, 21:29
par Arbre » 13 Jan 2017, 21:29
Par politesse je donne l'astuce de ma preuve : j'ai utilisé le théorème de point fixe de Picard.
Bonne soirée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
