salut tt l monde,
je m apelle karim et g vx votre aide s il vs plait,j ai un problem avec un
exercice de polynomes, voila la polynome:
Pn(x)=1/2^n[(x+ le racine carré de x²-1)^n + (x-le racine carré x²-1)^n ]
1) montre que pour tt n appartien à N-{1} on a :
Pn(x)-xPn-1(x)+1/4[Pn-2(x)]=0
2)monter que Pn est polynome et indiquer sa degré.(Pn="P" indice "n")
(remarque: utilise un des raisonnement logique)
bonne chance!!!!!!
Les polynomes
9 messages
- Page 1 sur 1
Salut karim
Pn(x)=1/2^n[(x+ le racine carré de x²-1)^n + (x-le racine carré x²-1)^n ]
et
Pn-1(x)=1/2^(n-1)[(x+ le racine carré de x²-1)^(n-1) + (x-le racine carré x²-1)^(n-1) ]
ensuite il faut faire le même type de remplacement pour Pn-2(x)
et puis ensuite remplacer
tout ça dans Pn(x)-xPn-1(x)+1/4[Pn-2(x)]
et essayer de trouver 0
oki ?
Pn(x)=1/2^n[(x+ le racine carré de x²-1)^n + (x-le racine carré x²-1)^n ]
et
Pn-1(x)=1/2^(n-1)[(x+ le racine carré de x²-1)^(n-1) + (x-le racine carré x²-1)^(n-1) ]
ensuite il faut faire le même type de remplacement pour Pn-2(x)
et puis ensuite remplacer
tout ça dans Pn(x)-xPn-1(x)+1/4[Pn-2(x)]
et essayer de trouver 0
oki ?
Mon avatar me fait peur, est-ce normal docteur ?
c'est un exo tres facile qui ne doit pas etre posté dans "olympiades"
tu as repondu a la 1er questio, c'est bien
je vais donc repondre a la 2eme question.
reccurence
on a=2,p_1(x)=x) qui sont des polynomes
qui sont des polynomes
soit tel que
tel que 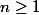
suppons que
on a=xP_{n}(x)-\frac{1}{4}p_{n-1}(x)) polynome (car
polynome (car  sont des polynomes)
sont des polynomes)
donc est un polynome.
est un polynome.
mtn on pose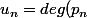)
on a=xP_{n+1}(x)-\frac{1}{4}p_n(x))
donc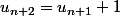 (car on a
(car on a \ge deg(p_n)) )
)
donc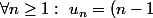+u_1=n) et
et 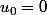
donc=n)
tu as repondu a la 1er questio, c'est bien
je vais donc repondre a la 2eme question.
reccurence
on a
soit
suppons que
on a
donc
mtn on pose
on a
donc
donc
donc
:id: mé monsieur, c'est vrai qe P1,P2,P3 sont des polynomes mé ça ne veux dire po que Pn-2 et Pn-1 seront des polynomes ,çaaaaaaaaaa vx dire que c'est po necessaire que Pn sera polynome aussi.g px te donner infini de polynome où ta mathode sera ineffecace.so c'est mieux que tu utilise le Raisonnement par récurrence :marteau:
karim_2007 a écrit::id: mé monsieur, c'est vrai qe P1,P2,P3 sont des polynomes mé ça ne veux dire po que Pn-2 et Pn-1 seront des polynomes ,çaaaaaaaaaa vx dire que c'est po necessaire que Pn sera polynome aussi.g px te donner infini de polynome où ta mathode sera ineffecace.so c'est mieux que tu utilise le Raisonnement par récurrence :marteau:
je vous consiel de voir la methode de recurrence forte avec ton prof. apres essaye de bien lire ma demo ok, :zen:
karim_2007 a écrit:ok amonsieur=(monsieur) ,ila jatt 3la khattrak=(si tu veus) tu peux m expliquer ta méthode s il vx plait mé g incicte à que tu utilise l reccurence.merci :++:
j'ai deja tous dit dans mon 1er poste et j'ai bien utilisé la reccurence forte,
alors tu n'a que lire ce document sur la reccurence forte
http://www.animath.fr/cours/recurrence.html
et apres il faut revoire ma demo.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
