Les nombres initiateurs

par **Mario2015** » 07 Juil 2015, 13:00

Prenez le nombre 1.

Si vous sommez les nombres de 1 a 3 en rajoutant a chaque fois 1 : 1+2+3=3! vous obtenez un nombre factoriel.

Le nombre 5

5+6+7+.......+98+99+100=7!

Le nombre 7

7+8+9=4!

Le nombre 30

30+31+32+33+.....+284+285 = 8!

Bref, il existe une infinite de nombres ayant les memes proprietes.
Appelons-les les nombres initiateurs et notons les "I". Donc 1,5,7,30 par exemple sont des nombres initiateurs.

S(I,k)=n! ou I est le nombre de depart, k la longueur de la suite et S(I,k) la somme des nombres consecutifs de I a (I+k-1)

La meme factorielle peut avoir plusieurs nombres initiateurs.

Le defi est simple :

-lister les 100 premiers nombres initiateurs
- trouver un algorithme pour savoir rapidement si un nombre est initiateur ou non?

par **Mario2015** » 07 Juil 2015, 14:28

Par exemple :

(n!/3)-1 est toujours un nombre initiateur

5!=120

(120/3)-1=39

39+40+41=120
Donc 39 est un nombre initiateur
De meme 239
239+240+241=720=6!

par **Mario2015** » 07 Juil 2015, 14:32

22 est un nombre initiateur :

S(22,5)=22+23+24+25+26=5!

par **Waax22951** » 07 Juil 2015, 15:59

Bonjour,
Je n'y ai pas du tout réfléchis, mais voici ce que j'ai trouvé:

Soit n un nombre initiateur. Par hypothèse, il existe un entier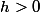

et un entier naturel p tels que:
[CENTER]

[/CENTER]

Soit encore:
[CENTER]

[/CENTER]

D'où:
[CENTER]

[/CENTER]

Il s'agit d'un trinôme du second degré dont l'unique racine pouvant être positive est:

[CENTER]

[/CENTER]

Donc

est un entier positif.

Réciproquement, s'il existe un entier p tel que

soit un entier positif, alors il est évident que

[CENTER]

[/CENTER]

Donc n est un nombre initiateur si, et seulement si il existe un entier p tel que:
[CENTER]

[/CENTER]

Autrement dit, n est un nombre initiateur si, et seulement si il existe un entier p tel que

soit impair.

Je ne sais pas si c'est très utile, mais dans le doute je te le donne..! :lol3:

Bonne journée !

par **Mario2015** » 07 Juil 2015, 17:18

Merci.
avec n=5 et p=7 ta forumle donne un nombre non entier
rac(11^2-40+8*7!)=201 et 201 n`est pas divisible par 8.

Or 5 est un nombre initiateur de 7!
Tu peux reverifier tes calculs stp?

Merci.

par **messinmaisoui** » 07 Juil 2015, 17:36

Bonjour Mario2015,

Intéressant comme sujet !

Mais qui ... quoi nous dit que par exemple 3 n'est pas un initiateur ?
Ainsi ... il n'existerait pas une suite telle que
3+4 + ... +1 000 0001 + 1 000 0002 + ... 1 000 000 0005 + 1 000 000 0006 + ... = x!
Vraiment ?

Mais comment le prouver ?

par **Mario2015** » 07 Juil 2015, 17:42

messinmaisoui a écrit:Bonjour Mario2015,

Intéressant comme sujet !

Mais qui ... quoi nous dit que par exemple 3 n'est pas un initiateur ?
Ainsi ... il n'existerait pas une suite telle que
3+4 + ... +1 000 0001 + 1 000 0002 + ... 1 000 000 0005 + 1 000 000 0006 + ... = x!
Vraiment ?

Mais comment le prouver ?

Exacte ta reflexion! C`est un peu la ou je voulais en venir.
Mon but etait de trouver un nombre particulier plus difficile a trouver qu`un nombre premier.
Pour un nombre premier, la recherche se fait en amont.
Quid d`un nombre ou la recherche se fait en aval.
La aussi il y a matiere a exclure certaines valeurs du champ des nombres initiateurs (un peu comme pour les nombres premiers le seul nombre pair premier est 2).
Y a-t-il des liens entre les nombres initiateurs?

par **Waax22951** » 07 Juil 2015, 17:46

Mario2015 a écrit:Merci.
avec n=5 et p=7 ta forumle donne un nombre non entier
rac(11^2-40+8*7!)=201 et 201 n`est pas divisible par 8.

Or 5 est un nombre initiateur de 7!
Tu peux reverifier tes calculs stp?

Merci.

Tu as raison, mon erreur est corrigée, enfin je crois :ptdr:

par **Mario2015** » 07 Juil 2015, 17:49

Theoreme simple :

Si 2k+1 divise n!
I= (n!/(2k+1))-k est toujours un nombre initiateur

par **Mario2015** » 07 Juil 2015, 17:53

Waax22951 a écrit:Tu as raison, mon erreur est corrigée, enfin je crois :ptdr:

Il y a toujours un probleme dans ta formule je crois.

par **Waax22951** » 07 Juil 2015, 18:04

Mario2015 a écrit:Il y a toujours un probleme dans ta formule je crois.

Ah bon ? x)
Décidément.. Par contre je ne vois pas le contre-exemple (enfin plutôt je ne peux pas le vérifier puisque je n'ai pas de feuille, de crayon ou de calculatrice ^^')

Bonne soirée !

par **zygomatique** » 07 Juil 2015, 18:17

salut

pour

:ptdr:

par **Mario2015** » 07 Juil 2015, 19:01

Partant d`un n donne le probleme reviendrait a resoudre une equation diophantienne a 2 variables p et h.
Peut-on conjecturer que tout entier n>0 peut etre un nombre initiateur?
Plus p! est grand plus le nombre de nombres initiateurs solution croit.
Estimer la croissance du nombre de solutions peut etre interessant pour voir plus clair.
Arithmeticiens et programmeurs a vos ordinateurs!

par **zygomatique** » 07 Juil 2015, 19:25

pour simplifier la formule de waax ...

le discriminant est

on peut alors remarquer que

est impair donc s'il est le carré d'un entier alors cet entier est impair et h est bien entier ...

et donc

...

par **paquito** » 07 Juil 2015, 20:59

Soit p un entier quelconque>1, il existe toujours des nombres I, initiateurs de p!

soit n la longueur de l'écriture:

lorsque l'on veut n pair et

, si l'on veut n impair avec la condition

ou

exemple: p=11; n=4 ; I=7983558;I+I+1+...+I+4=11!

p=11, n=7;I=5702397 et I+I+1+....+I+6=11!

Conclusion: on peut fixer un peu comme on veut p et n; I se calcule facilement; quant à savoir si I est initiateur, je ne vois pas l'intérêt!

par **Mario2015** » 07 Juil 2015, 21:22

paquito a écrit:Soit p un entier quelconque>1, il existe toujours des nombres I, initiateurs de p!

soit n la longueur de l'écriture:

lorsque l'on veut n pair et
, si l'on veut n impair avec la condition ou

exemple: p=11; n=4 ; I=7983558;I+I+1+...+I+4=11!

p=11, n=7;I=5702397 et I+I+1+....+I+6=11!

Conclusion: on peut fixer un peu comme on veut p et n; I se calcule facilement; quant à savoir si I est initiateur, je ne vois pas l'intérêt!

I=3 a quoi est egal p?

par **Mario2015** » 07 Juil 2015, 21:25

Savoir si un nombre est initiateur ou non a plus d`interet que tu ne penses monsieur Paquito.
Tu ne fais que reprendre ma formule donnee plus haut.
Toute factorielle a au moins un initiateur.
Est-ce que tout nombre entier I > 0 conduit a factorielle?
Je ne le sais pas.
Et je ne peux pas le prouver.

par **Doraki** » 07 Juil 2015, 21:44

Tu n'as pas montré que 6,8,9,10,... étaient pas initiateurs ?

Je pense avoir un algorithme qui dit si un nombre est initiateur ou pas.

par **Mario2015** » 07 Juil 2015, 22:16

Doraki a écrit:Tu n'as pas montré que 6,8,9,10,... étaient pas initiateurs ?

Je pense avoir un algorithme qui dit si un nombre est initiateur ou pas.

J`ai deja dit que je ne le savais pas.
Un algo qui dirait 3 est un nombre initiateur ou pas serait le bienvenu.
On peut produire des initiateurs avec toute sorte de suites (arithmetiques raison > 1 par exemple etc...)

par **Doraki** » 08 Juil 2015, 09:08

bon en fait je me suis embrouillé, finalement j'ai rien

Les nombres initiateurs

Les nombres initiateurs

Qui est en ligne