Soit
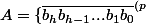}=\sum_{k=0}^h{b_kp^k},h\geq 0,0\leq b_k \leq p-2\})
Le but est de montrer que

est le n ieme terme de A.
Propriété 1:A ne contient pas de progressions arithmétiques de longueur p
Preuve:Soit
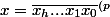})
et
})
2 entiers >0 décomposés en base p.Montronss que les x+mu,
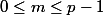
ne peuvent etre tous dans A.Si d est le plus petit entier tel que

,dans la décomposition
})
,on a

mod p.
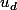
etant non nul donc inversible modulo p,on peut trouver
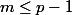
tel que
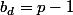
et alors x+mu n est pas dans A
Propriéte 2:Si x n est pas dans A, on peut trouver une progression arithmetique de longueur p finissant par x et telle que les p-1 premiers termes soient dans A.
Preuve:Ecrivons
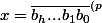}=\sum_{k=0}^h{b_kp^k})
et posons:
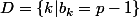
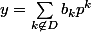

Alors pour
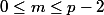
,y+mu est dans A et y+(p-1)u=x
Le résultat découle alors des propriétés 1 et 2 par une reccurence directe:
Supposons avoir montrer que a_k est le k-ieme terme de A pour k=1,...,n-1
Comme A ne contient de suite arith de longueur p(propriété 1),

est plus petit que le n-ieme terme de A.De plus

est dans A sinon on obtiendrait une absurdité par la propriété 2.Donc

est le n-ieme terme de A..