Comme je l'ai écrit on peut faire plus simple, abordable au niveau terminale.
Il y a par ex la démo utilisant la symétrie de Steiner .. passons ..
Mais voici celle qui est la plus simple dont j'ai apris l'existence l'année dernière, bien qu'elle datât si je ne me trompe pas de 1953(Littlewood) !
Soit

un point où il y a une tangente à la courbe

. On prend

comme origine et la tangente comme axe des
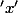
, la courbe étant au dessus. (désolé je ne sais pas faire des figures

)
Soit
,t\in [0,\pi])
, l'équation de la courbe en coordonnées polaires.
La surface du domaine entouré par la courbe est alors :
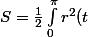dt=\frac 12\int_0^{\pi/2}(r^2(t)+r^2(t+\pi/2))dt)
Le triangle
)O(0,0)N(t+\pi/2,r(t+\pi/2)))
est manifestement rectangle donc
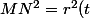+r^2(t+\pi/2))
Mais
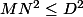
(rappel

est le "diamètre" du domaine).
Il s'ensuit
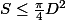
donc
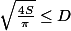
.. q.e.d
L'égalité a lieu seulement pour le cercle (je vous laisse le prouver) ..



