Montrer que
Intervalle
7 messages
- Page 1 sur 1
Intervalle
par MMu » 10 Déc 2018, 19:44
Soient les rééls positifs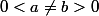 
et l'ensemble de rééls positifs }=\{xy; 0<x\neq y>0,x^a-y^a=x^b-y^b\})
Montrer que})
est un intervalle ouvert et déterminer ses bornes.
Montrer que
Re: Intervalle
par Ben314 » 10 Déc 2018, 20:20
Salut,
\!-\!\ln(a)}{b-a})
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intervalle
par aviateur » 10 Déc 2018, 22:54
Bonjour
Pour le pourquoi:
On peut supposer 0<a<b.
Si on pose=u^a-u^b)
et sans restreindre la généralité on supposera x<y lorsque f(x)=f(y).
Une étude de la fonction montre que la fonction f est croissante sur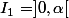
puis décroissante sur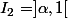 
avec)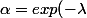
. On pose )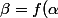
On désigne par (g resp. h) la fonction réciproque de f restreinte à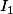
(resp. 
)
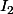Alors S est l'image de)
par la fonction gh. Cette fonction est dérivable et un calcul de sa dérivée montre que cette fonction est croissante.
On en déduit que[)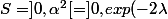
Pour le pourquoi:
On peut supposer 0<a<b.
Si on pose
Une étude de la fonction montre que la fonction f est croissante sur
avec
On désigne par (g resp. h) la fonction réciproque de f restreinte à
Alors S est l'image de
On en déduit que
Re: Intervalle
par MMu » 13 Déc 2018, 04:28
Bien Aviateur, c'est bien de donner une preuve.
Je trouve que donner juste le résultat n'est pas très intéressant.
Voici ma démarche. Comme Aviateur , et sans perte de généralité , je considère
.
On pose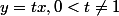
et on arrive à =x^b(1-t^b))
Il s'ensuit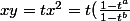^{\frac 2{b-a}}=(\frac {t^a-t^{-a}}{t^b-t^{-b}})^{\frac 2{b-a})
Il suffit d'étudier la fonction=\frac {t^a-t^{-a}}{t^b-t^{-b}})
(classique connu) . Pour le fun je le fait.
On arrive facilement (Hôpital, etc ..) à=0,\ \lim_{t\rightarrow 1}f(t)=\frac ab)
Ensuite en utilisant le développement en série on obtient :
=\frac {\sum_{n=0}^{\infty}(a\ln t)^{2n+1}/((2n+1)!)}{\sum_{n=0}^{\infty}(b\ln t)^{2n +1}/((2n+1)!)}=<br />\frac ab \frac {\sum_{n=0}^{\infty}(a\ln t)^{2n}/((2n+1)!)}{\sum_{n=0}^{\infty}(b\ln t)^{2n }/((2n+1)!)}< \frac ab)
Tout ceci montre que l'intervalle pour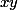
est ^{\frac 2{b-a}}[)
Je trouve que donner juste le résultat n'est pas très intéressant.
Voici ma démarche. Comme Aviateur , et sans perte de généralité , je considère
On pose
Il s'ensuit
Il suffit d'étudier la fonction
On arrive facilement (Hôpital, etc ..) à
Ensuite en utilisant le développement en série on obtient :
Tout ceci montre que l'intervalle pour
Re: Intervalle
par descampsh » 13 Déc 2018, 09:23
En mathématique, les démarches possèdent aussi une grande importance pour bien comprendre les résultats.
Re: Intervalle
par MMu » 13 Déc 2018, 12:01
MMu a écrit:Bien Aviateur, c'est bien de donner une preuve.
Je trouve que donner juste le résultat n'est pas très intéressant.
Voici ma démarche. Comme Aviateur , et sans perte de généralité , je considère
On pose
Il s'ensuit
Il suffit d'étudier la fonction(classique connu) . Pour le fun je le fait.
On arrive facilement (Hôpital, etc ..) à
Ensuite en utilisant le développement en série on obtient :=\frac {\sum_{n=0}^{\infty}((a\ln t)/2)^{2n+1}/((2n+1)!)}{\sum_{n=0}^{\infty}((b\ln t)/2)^{2n +1}/((2n+1)!)}=<br />\frac ab \frac {\sum_{n=0}^{\infty}((a\ln t)/2)^{2n}/((2n+1)!)}{\sum_{n=0}^{\infty}((b\ln t)/2)^{2n }/((2n+1)!)}< \frac ab)
Tout ceci montre que l'intervalle pour
J'ai corrigé une faute de frappe
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :