Soient
Montrer que
On supposera démontrée la convergence de cette intégrale. (qu'il l'est d'ailleurs)
Bonne chance.
Thomas :zen:
Intégrales
13 messages
- Page 1 sur 1
Intégrales
par nekros » 14 Juil 2006, 00:22
Bonsoir,
Soient
et 
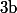
dans 
.
Montrer que})
On supposera démontrée la convergence de cette intégrale. (qu'il l'est d'ailleurs)
Bonne chance.
Thomas :zen:
Soient
Montrer que
On supposera démontrée la convergence de cette intégrale. (qu'il l'est d'ailleurs)
Bonne chance.
Thomas :zen:
par aviateurpilot » 14 Juil 2006, 00:49
là
je n'ai rien a dire
car je n'ai pas encore vu une integrale de cette forme dans le cour( :hein: )
je n'ai rien a dire
car je n'ai pas encore vu une integrale de cette forme dans le cour( :hein: )
par mln » 14 Juil 2006, 01:19
Juste une idée sans etre rigoureux :
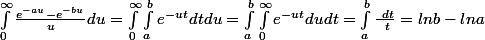
(je n'est pas prouvé qu'on pouvait inverser... mais j'imagine qu'on peut)
(je n'est pas prouvé qu'on pouvait inverser... mais j'imagine qu'on peut)
par Nightmare » 14 Juil 2006, 01:46
Bonsoir tout le monde :happy3:
mln : L'inversion vient du théorème de fubini si je ne me trompe pas.
Sinon la convergence de l'intégrale, même si elle est admise, se démontre aisément me semble-t-il :
u²f(u) (ou f(u) est l'intégrande) converge vers 0 lorsque u->+oo, c'est un critère de convergence qui permet donc d'affirmer que notre intégrale converge (absolument même)
:happy3:
mln : L'inversion vient du théorème de fubini si je ne me trompe pas.
Sinon la convergence de l'intégrale, même si elle est admise, se démontre aisément me semble-t-il :
u²f(u) (ou f(u) est l'intégrande) converge vers 0 lorsque u->+oo, c'est un critère de convergence qui permet donc d'affirmer que notre intégrale converge (absolument même)
:happy3:
par Sdec25 » 14 Juil 2006, 01:47
Je crois qu'on peut inverser quand les bornes de l'intégrales de dépendent pas de la variable d'intégration de l'autre intégrale (théorème de Fubini je crois).
par mln » 14 Juil 2006, 09:15
Merci Nightmare, je pensais que Fubini ne suffisait quand on intègre par rapport à u sur 
: je me serais embêté à faire :
dt du=lim_{c->+\infty} \int_a^b\int_0^c f(u,t)du dt = \int_a^b lim_{c->+\infty} \int_0^c f(u,t)dt du)
en justifiant l'inversion limite et intégrale. :we:
par Chimomo » 14 Juil 2006, 10:38
Fubini est fait pour éintervertir les intégrales sur des intervalles autre qu'un segment (parceque pour deux segments il est assez évident). Cependant, il faut faire attention, il y a plein d'hypothèses à vérifier pour appliquer le théorème de Fubini !
par nekros » 14 Juil 2006, 10:52
Bonjour tout le monde,
C'est vrai que la convergence (et donc le fait que l'intégrale existe) est facile à prouver.
En effet, on a=\frac{exp{-au}}{u}+\frac{exp{-bu}}{u}=o(\frac{1}{u^2}))
Donc à partir d'un certain rang, on a :| \le \frac{1}{u^2})
et on conclut avec la comparison des intégrales à termes positifs
(
: Riemann)
Thomas G :zen:
C'est vrai que la convergence (et donc le fait que l'intégrale existe) est facile à prouver.
En effet, on a
Donc à partir d'un certain rang, on a :
(
Thomas G :zen:
par nekros » 14 Juil 2006, 10:57
Sinon pour l'exo, penser à faire un changement de variable, utiliser la linéarité de l'intégrale...
Thomas G :zen:
Thomas G :zen:
par nekros » 15 Juil 2006, 02:54
Salut, une correction possible :
On pose=\frac{exp{-au}-exp{-bu}}{u}})
On commence par calculer du)
En posant respectivement
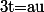
et 
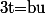
, on a :
 du = \int_a^{b} \frac{exp{-t}}{t}dt)
Par ailleurs, on remarque que=\int_a^{b} \frac{dt}{t})
.
En outre,du = \int_0^{1}f(u)du-\int_1^{+\infty}f(u)du})
Il faut donc montrer quedu=ln(\frac{b}{a})-\int_1^{+\infty}f(u)du=\int_a^{b}\frac{1-exp{-t}}{t} dt)
Allons-y :
du=\int_0^{1} \frac{exp{-au}-1}{u}+\frac{1-exp{-bu}}{u} du=-\int_0^{1}\frac{1-exp{-au}}{u}du+\int_0^{1}\frac{1-exp{-bu}}{u}du)
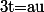
Or, en posant, on a 
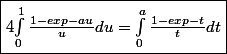
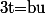
De même, en posant, on a 
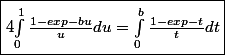
Finalement,du=-\int_0^{a}\frac{1-exp{-t}}{t}dt+\int_0^{b}\frac{1-exp{-t}}{t}dt=\int_a^{b}\frac{1-exp{-t}}{t}dt)
CQFD
Thomas G :zen:
On pose
On commence par calculer
En posant respectivement
Par ailleurs, on remarque que
En outre,
Il faut donc montrer que
Allons-y :
Or, en posant
De même, en posant
Finalement,
CQFD
Thomas G :zen:
par Nightmare » 15 Juil 2006, 11:00
La démonstration par fubini est tout de même plus simple et naturelle :lol3:
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :