Infinité de solutions
Olympiades mathématiques, énigmes et défis
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 03 Nov 2007, 13:58
par lapras » 03 Nov 2007, 13:58
Bonjour,
je vous propose un exercice :
Montrer qu'il existe une infinité de triplets (m,n,p)
tels que
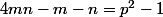
Bon courage
:happy2:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 03 Nov 2007, 14:52
par lapras » 03 Nov 2007, 14:52
oui :happy2:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 03 Nov 2007, 16:20
par lapras » 03 Nov 2007, 16:20
Bravo :happy2:
Maintenant il faut démontrer qu'il n'y a pas de triplets (m,n,p) tels que
4mn - m - n = p²
:happy2:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Nov 2007, 23:49
par aviateurpilot » 03 Nov 2007, 23:49
supposons que
:\ p^2=4mn-m-n)
on a donc
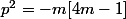
puisque
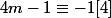
donc il exists un premie
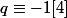
tel que
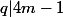
(
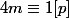
)
donc on a
^2=4p^2\equiv -4m[q]\equiv -1[q])
^2)^{\frac{q-1}{2}}=\equiv (-1)^{\frac{q-1}{2}}[q]\equiv -1[q])
(car
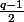
impair)
d'ou
^{q-1}\equiv -1[q])
(absurde)

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 04 Nov 2007, 02:33
par raito123 » 04 Nov 2007, 02:33
bah je sui ravi qu'il y a des gens comme toi ziz
lol je vais faire mon mieux pour devenir ds la meme hauteur que vous :ptdr: lol
Les multiples ne doivent pas être utilisés sans nécessité
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 04 Nov 2007, 10:12
par lapras » 04 Nov 2007, 10:12
Bravo aviateurpilot ! :++: :we:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 04 Nov 2007, 11:42
par yos » 04 Nov 2007, 11:42
Si Aviateurpilote pouvait corriger les p qui sont en fait des q (à cinq endroits seulement), ce serait parfait.
Sinon l'égalité
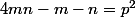
entraîne
(4n-1)=4p^2+1)
et on en déduit comme Aviateurpilote l'existence d'un diviseur premier

de
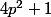
qui serait congru à -1 modulo 4. Il est connu que c'est impossible (voir la preuve classique de l'infinité des nombres premiers de la forme 4n+1) et la preuve de ce dernier fait utilise le petit théorème de Fermat. Bref, c'est ce qu'a fait Aviateurpilote.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 04 Nov 2007, 13:12
par aviateurpilot » 04 Nov 2007, 13:12
salut
lapras si tu veus la demo de
premierment on montre que
!\equiv -1[p])
on sais bien que
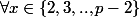
il existe un unique
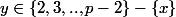
tel que
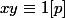
on peus donc pendre la bijection
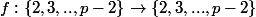
tel que
\equiv 1[p])
on a donc
!\equiv 1[p])
car dans le produit (p-2)! chaque facteur

a son invers propre
)
dont le produit donne
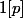
et donc
!=(p-1)(p-2)!\equiv (p-1)\times 1[p])
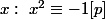
=>
^{\frac{p-1}{2}}\equiv (x^2)^{\frac{p-1}{2}}\equiv 1[p])
=>
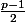
pair
=>
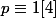
et
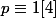
=>
!=\prod_{a=1}^{\frac{p-1}{2}}a(p-a)\equiv \prod_{a=1}^{\frac{p-1}{2}}-a^2[p]\equiv (-1)^{\frac{p-1}{2}}(\(\frac{p-1}{2}\)!)^2 [p])
=>
!)^2 \equiv (p-1)![p]\equiv -1[p])
=>
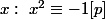
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 04 Nov 2007, 13:22
par lapras » 04 Nov 2007, 13:22
Tres jolie démo, merci aziz, je penserai a toi quand je m'en re-servirai ! :we:
PS : tu as re démontré le théoreme de wilson ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités