Soit x,y,z des réels positifs tels que
x + y + z = 3
Montrer que
Bonne chance ! :we:
Inégalité
24 messages
- Page 1 sur 2 - 1, 2
par Imod » 13 Avr 2008, 10:02
Une démonstration facile avec l'inégalité des moyennes arithmétiques et géométriques :
On a donc-2(\sqrt{x}+\sqrt{y}+\sqrt{z}))
Et comme^2-2(xy+yz+xz))
, on a l'inégalité voulue .
Imod
On a donc
Et comme
Imod
par vincent.pantaloni » 13 Avr 2008, 10:20
Bien vu Imod, j'avais cherché avec moy arith et geom mais j'avais pas trouvé. Bravo.
par lapras » 21 Avr 2008, 20:27
Autre inégalité plus facile :
soit a,b,c des réels positifs tels que a²+b²+c²=3
Montrer que
1/(1+ab) + 1/(1+ac) + 1/(1 + bc) >= 3/2
par Mhdi » 27 Avr 2008, 10:32
Ma méthode n'est pas aussi élégante que celle d' Imod, mais je pense que c'est correct.
D'après l'inégalité de la moyenne :
(1+ac)(1+bc)})^1/3)
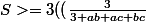On applique une deuxième fois l'inégalité de la moyenne :^3)1/3)
=>)
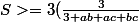On sait que
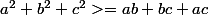
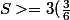Donc=3/2)
D'après l'inégalité de la moyenne :
On applique une deuxième fois l'inégalité de la moyenne :
=>
On sait que
Donc
par lapras » 28 Avr 2008, 10:35
Excellent
L'idée était l'inégalité moyenne harmonique/moyenne arithmétique
L'idée était l'inégalité moyenne harmonique/moyenne arithmétique
par lapras » 03 Mai 2008, 20:30
Si je dois avoir ca mais je ne les ai pas encore cherchées donc :
-Je n'ai pas la solution si personne ne trouve (ca m'étonnerait !)
-Répondez en blanc s.v.p car je n'aimerai pas voir la solution.
Ces inégalités sont dans mon post récent des olympiades : "16 exercices tres interessants"
-Je n'ai pas la solution si personne ne trouve (ca m'étonnerait !)
-Répondez en blanc s.v.p car je n'aimerai pas voir la solution.
Ces inégalités sont dans mon post récent des olympiades : "16 exercices tres interessants"
par Mhdi » 03 Mai 2008, 21:39
Tu peux poster ta solution en utilisant la moyenne harmonique/moyenne arithmétique?
par mehack » 26 Mai 2008, 10:37
slt !!
Caushy shwartz kill it :zen:
+(1+ac)+(1+bc))(\frac{1}{1+ab}+\frac{1}{1+ac}+\frac{1}{1+bc})\geq 9)
donc il suffit de montrer :
equivaut :
ce qui est vrai puisque
Caushy shwartz kill it :zen:
donc il suffit de montrer :
equivaut :
ce qui est vrai puisque
par mehack » 26 Mai 2008, 10:45
une autre inegalité : (à ne pas sousestimer :id: )
a,b,c des reels positifs tel que abc=< 1 , MQ :
a,b,c des reels positifs tel que abc=< 1 , MQ :
par lapras » 26 Mai 2008, 17:53
Salut,
l'inégalité est symétrique, on peut poser :
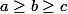
L'inégalité se réécrit :
 + ab^{2}(1-c) + bc^{2}(1-a) \geq 0)
Or moyenne harmonique/géométrique =>
^{\frac{1}{3}} \geq \frac{3}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}} = \frac{3abc}{ab+ac+bc} ab(1-c)+ac(1-b)+bc(1-a)\geq0)
soit en multipliant par c :
 + ab^{2}(1-c) + bc^{2}(1-a) \geq abc(1-c) + ac^2(1-b) + bc^2(1-a)\geq0)
d'où le résultat
l'inégalité est symétrique, on peut poser :
L'inégalité se réécrit :
Or moyenne harmonique/géométrique =>
soit en multipliant par c :
par Mhdi » 26 Mai 2008, 18:14
lapras>> Je n'ai pas compris la dernière ligne de ta démo : tu multiplies par a, donc tu obtiens +a^{2}c(1-b)+abc(1-a) \geq 0)
et+a^{2}c(1-b)+abc(1-a) \geq a^{2}c(1-b) + ab^{2}(1-c) + bc^{2}(1-a))
Mais on ne peut pas en déduire que+a^{2}c(1-b)+abc(1-a) \geq a^{2}c(1-b) + ab^{2}(1-c) + bc^{2}(1-a)\geq0)
, non?
et
Mais on ne peut pas en déduire que
par Mhdi » 26 Mai 2008, 18:57
Ok ! :++:
On peut peut-être s'y prendre autrement : abc=<1, donc au moins un de ces nombres est =< 1. Je ne sais pas si ça peut marcher (j'ai fait quelques vaines tentatives), mais peut-être que cette "remarque" peut servir. ;)
On peut peut-être s'y prendre autrement : abc=<1, donc au moins un de ces nombres est =< 1. Je ne sais pas si ça peut marcher (j'ai fait quelques vaines tentatives), mais peut-être que cette "remarque" peut servir. ;)
par mehack » 26 Mai 2008, 20:57
ThSQ a écrit:( Elle est dans le poly de Pierre Bornsztein sur animath. )
nn je n crois pas car jé cherché dans le e-book de bronznstein !!
en tt cas l inegalité existe partout avec abc=1 mais moi jé ajouté ma touche personelle abc=<1 . je crois qu ell a maintenant un look facile mais elle n est pas si simple que ca :++:
par Zweig » 26 Mai 2008, 22:18
D'après l'inégalité arithmético-géométrique :
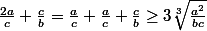
Or
=> 
, d'où 
De même,
Après somme de ces trois inégalités, on obtient le résultat désiré.
Or
De même,
Après somme de ces trois inégalités, on obtient le résultat désiré.
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :