allez un pti problème qui vient de Tangente sup magazine!
Montrer que pour tout x,y,z R+ tels que xyz=1
Bonne chance :we:
Inégalité
11 messages
- Page 1 sur 1
par abel » 03 Oct 2006, 21:18
Il manque pas des conditions sur x,y,z car si on prend x=y=z=0 ca marche pas
par Help » 09 Oct 2006, 12:42
Tu es certain qu'il n'y a pas une autre condition sur x,y,z (du genre tous positifs) ? Avec x=-1.5, et y=3 (et donc z = -2/9), cela donne un résultat négatif...
par darkmaster » 05 Déc 2006, 11:08
On pose 
On a
(1+z) } + \frac { y^3 } { (1+z)(1+x) } + \frac { z^3 } { (y+1)(1+x) }= \sum\frac { x^3 } { (1+y)(1+z) }=\sum\frac{u^{10}}{(uv+t^2)(ut+v^2))
En utilisant Cauchy-Schwarts inégalité:
(ut+v^{2})}}\geq \frac{(\sum{u^{5}})^{2}}{\sum{(uv+t^{2})(ut+v^{2})}})
On a \geq \frac13(u^4+v^4+t^4)(u+v+t))
(chebyshev inégalité)
alors^2 \geq \frac13(u^4+v^4+t^4)(u+v+t)(u^5+v^5+t^5))
Mais\geq 3)
et \geq 3)
(car 
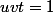
) alors ^2\geq 3(u^4+v^4+t^4))
Il reste à montrer que\geq \frac34 \sum{(uv+t^{2})(ut+v^{2}))
qui est vrai par mürhead inégalité.
On a
En utilisant Cauchy-Schwarts inégalité:
On a
alors
Mais
Il reste à montrer que
par khaclong » 20 Déc 2006, 23:55
salut,je viens de trouver une autre solution pour ce problème
(1+z)}+\frac{1+y}{8}+\frac{1+z}{8}\geq 3\sqrt[3]{\frac{x^3}{(1+y)(1+z)}\frac{1+y}{8}\frac{1+z}{8}}=\frac34x)
(1+z)}+\frac{1+x}{8}+\frac{1+z}{8}\geq 3\sqrt[3]{\frac{y^3}{(1+x)(1+z)}\frac{1+x}{8}\frac{1+z}{8}}=\frac34y)
(1+y)}+\frac{1+y}{8}+\frac{1+x}{8}\geq 3\sqrt[3]{\frac{z^3}{(1+x)(1+y)}\frac{1+y}{8}\frac{1+x}{8}}=\frac34z)
Ensuite,on prend la somme de ces inégalités,on aura
(1+z)}+\frac{y^3}{(1+x)(1+z)}+ \frac{z^3}{(1+x)(1+y)}+\frac{3}{4}+\frac{x+y+z}{4}\geq \frac34(x+y+z))
alors,on a
(1+z)}+\frac{y^3}{(1+x)(1+z)}+ \frac{z^3}{(1+x)(1+y)}\geq\frac12(x+y+z)-\frac34\geq\frac32\sqrt[3]{xyz}-\frac34\geq\frac34)
c'est fini
Ensuite,on prend la somme de ces inégalités,on aura
alors,on a
c'est fini
par darkmaster » 24 Déc 2006, 10:58
khaclong a écrit:salut,je viens de trouver une autre solution pour ce problème
Ensuite,on prend la somme de ces inégalités,on aura
alors,on a
c'est fini
Et c'est beaucoup meilleur que ma mienne, Bravo
par samir » 29 Déc 2006, 12:33
On pose
(1+z)}+\frac{y^3}{(1+x)(1+z)}+\frac{z^3}{(1+x)(1+y)})
.
Par symétrie on suppose que
.
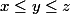
Alors(1+y) \leq (1+x)(1+z) \leq (1+y)(1+z))
et en appliquant l'inégalité de tchebychef on trouve
(\frac{1}{(1+x)(1+z)}+\frac{1}{(1+y)(1+z)}+\frac{1}{(1+x)(1+y)}))
.
On pose
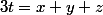
. On a alors (I.A.G) 
car 
,
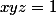
Et d'aprés (I.A.G),(1+y)(1+z) \leq (1+t)^3)
Donc^3} \geq \frac{3}{4})
car t --->^3})
croissante
pour
.
Par symétrie on suppose que
Alors
et en appliquant l'inégalité de tchebychef on trouve
On pose
Et d'aprés (I.A.G),
Donc
car t --->
pour
par dragonmaster » 08 Jan 2007, 00:14
J'ai une autre solution .
(1+z)} =\displaystyle \sum_{sym}\frac {x^4}{x(1+y)(1+z)}\geq \frac {(x^2+y^2+z^2)^2}{\displaystyle\sum_{sym} x(1+y)(1+z)})
(Buniacopsky inégalité)
Maintenant , on montre que
^2 \geq 3 \displaystyle\sum_{sym} x(1+y)(1+z) = 3(x+y+z)+6(xy+yz+zx)+9)
On a :
^2 \geq 9)
^2 \geq 2(xy+yz+zx)(x^2+y^2+z^2) \geq 6(xy+yz+zx))
^2 \geq \frac{1}{3} (x^2+y^2+z^2)(x+y+z)^2 \geq 3(x+y+z))
3 inégalités dernière utilisent Cauchy inégalité . C'est fini .
Maintenant , on montre que
On a :
3 inégalités dernière utilisent Cauchy inégalité . C'est fini .
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :