Inégalité!!
Olympiades mathématiques, énigmes et défis
-
Mohamed
- Membre Relatif
- Messages: 225
- Enregistré le: 02 Juil 2006, 21:01
-
 par Mohamed » 29 Juil 2006, 21:56
par Mohamed » 29 Juil 2006, 21:56
bonsoir tt le monde. voici une inégalité :
Soit a,b,c des réels positifs non nuls tel que abc=1
Prouver que
} + \frac{1}{b^3(c+a)} + \frac{1}{c^3(a+b)} \geq 3/2)
BNE CHANCE :ptdr:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 30 Juil 2006, 00:42
par nada-top » 30 Juil 2006, 00:42
HOLA :ptdr:
par symétrie de rôle on suppose que


(1)
(c'est facile à voir) ..et on a d'aprés CAUCHY-SCHWARZ on a :
 ((b+c)+(a+c)+(a+b)) \geq (3)^2 =9)
(*) ( démo. si on pose

et
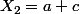
et

alors
(\frac{1}{X_1}+\frac{1}{X_2}+\frac{1}{X_3}\geq (\sum_{i=1}^{3} (\sqrt{X_i}.\frac{1}{\sqrt{X_i} } )^2) = 3^2=9)
)
et on a

(2)..donc de (1) et (2) et selon l'inégalité de Shybechev on
} + \frac{1}{b^3(a+c)} + \frac{1}{c^3(a+b)} \geq \frac{1}{3} (\frac{1}{a^3} + \frac{1}{b^3} + \frac{1}{c^3} ))
)

} + \frac{1}{b^3(a+c)} + \frac{1}{c^3(a+b)} \geq \frac{1}{3} (\frac{a^3b^3 +b^3c^3+ a^3c^3}{(abc)^3} ))
;(abc=1))

} + \frac{1}{b^3(a+c)} + \frac{1}{c^3(a+b)} \geq \frac{1}{3} (a^3b^3 +b^3c^3+ a^3c^3 ))
)
et puisque
\geq (a+b+c))
(**)
donc de (*) et (**) on déduit :
} + \frac{1}{b^3(a+c)} + \frac{1}{c^3(a+b)} \geq \frac{1}{3} (a+b+c) \frac{9}{2(a+b+c)})
d'ou le resultat
} + \frac{1}{b^3(a+c)} + \frac{1}{c^3(a+b)} \geq \frac{3}{2})
( ouuuf enfin.. ce latex est vraiment pénible

, j'espère au moins que c'est juste )
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 30 Juil 2006, 13:50
par nada-top » 30 Juil 2006, 13:50
( ouuuf enfin.. ce latex est vraiment pénible , [FONT=Comic Sans MS]j'espère au moins que c'est juste[/FONT]:soupir2: )
:soupir2: :soupir2: il y a personne ici pour rectifier ...il y a une grosse faute la haut ..je vais voir comment je peux régler :--:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Aoû 2006, 09:31
par nada-top » 01 Aoû 2006, 09:31
-
robin
- Membre Naturel
- Messages: 12
- Enregistré le: 01 Mai 2005, 01:14
-
 par robin » 01 Aoû 2006, 10:48
par robin » 01 Aoû 2006, 10:48
Bonjour,
C'est la même chose, mais pourquoi utiliser
}=\frac {\frac {1}{a^2}}{\frac {1}{b}+\frac {1}{c}})
? Comme abc=1,

. Alors d'après l'inégalité de Cauchy Shwarz :
})(\sum a(b+c)) \geq (\sum ab)^2)
ce qui est équivalent à :
} \geq \frac {\sum ab}{2} = \frac {3(abc)^{2/3}}{2}=\frac {3}{2})
.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Aoû 2006, 11:02
par nada-top » 01 Aoû 2006, 11:02
Hola
tu l'as dis
C'est la même chose
..et moi j'ai fait ça juste pour simplifier car j'ai pas encor étudié par exemple la dernière forme que tu as utilisé avec la puissance 2/3 ...(je suis encore en première)
-
robin
- Membre Naturel
- Messages: 12
- Enregistré le: 01 Mai 2005, 01:14
-
 par robin » 01 Aoû 2006, 11:18
par robin » 01 Aoû 2006, 11:18
bonjour
En fait
^{2/3})
c'est juste
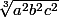
.
(moi aussi je suis en première)
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 01 Aoû 2006, 11:25
par nada-top » 01 Aoû 2006, 11:25
:ptdr: merci je savais pas je vais m'en servir next time
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités