Inégalité

par **atreyyu** » 16 Oct 2010, 20:16

J'ai besoin d'un conseil pour aborder cette inégalité:
Sachant que

, résoudre

.

par **Olympus** » 16 Oct 2010, 22:16

Salut !

Es-tu de la Pologne ? :ptdr:

par **atreyyu** » 16 Oct 2010, 22:28

Je viens de la Croatie, pourquoi demandes-tu ?

par **derivcompo** » 16 Oct 2010, 22:28

Bonsoir,

Je ne suis pas sûre de mon coup, mais pour commencer, si tu simplifiais en utilisant l'expression conjuguée chaque expression ?

par **Olympus** » 16 Oct 2010, 22:35

Ah, parce que cette inégalité vient du test MO de Pologne qui a eu lieu entre le 5 Octobre et le 4 Novembre ( et bon nombre de "tricheurs" demandaient sur le forum Mathlinks pendant cette période là ) .

Sinon, cette inégalité ne m'a pas l'air triviale, je vais essayer de passer cette nuit dessus et voir si je trouve quelque chose .

EDIT : corrigé les dates .

par **atreyyu** » 16 Oct 2010, 22:41

"MO", c'est quoi ? tricheurs ?

en utilisant l'expression conjuguée chaque expression ?

je ne suis pas tres sur comment le comprendre le mot "conjuguée", mais j'ai essayé d'atteindre en quelque forme

, mais en vain

par **Olympus** » 16 Oct 2010, 22:44

MO = Mathematical Olympiads .

Pour le sujet de ce test en cours, voir l'exercice 6 de ce .pdf : http://www.mimuw.edu.pl/~wwwom/zadania/om/om62_1.pdf .

par **derivcompo** » 16 Oct 2010, 22:47

atreyyu a écrit:"MO", c'est quoi ? tricheurs ?

je ne suis pas tres sur comment le comprendre le mot "conjuguée", mais j'ai essayé d'atteindre en quelque forme , mais en vain

Bof, je t'ai dit ça à la va-vite, mais en utilisant l'expression conjuguée tu pourrais enlever les racines du dénominateur pour les mettre au numérateur. Mais je pense que c'esten vain ! :briques:

par **atreyyu** » 16 Oct 2010, 22:52

Mmm, je ne comprends pas trop, mais évidemment c'est la même chose :--:
On nous donne un ensemble de ~100-120 problèmes chaque mois à résoudre pendant notre temps libre, à améliorer la compréhension de maths et la capacite de penser - les enseignants disent que ces tâches ne nécessitent pas beaucoup de lois théorèmes élaborés. Mais nous ne parlons pas de ces problemes dans la classe du tout, alors je n'ai vraiment personne à qui demander du conseil.

par **Olympus** » 17 Oct 2010, 20:40

Bon, j'ai trouvé qu'il suffirait de prouver l'inégalité suivante qui est plus forte en plus d'être homogène ( Wolfram me dit que le minimum du membre de gauche est

pour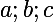

positifs, donc cela vaut peut-être la peine d'essayer ) :

.

Je la laisserai à quelqu'un de plus doué, j'ai passé tout mon temps depuis hier sans trouver vu que je n'ai travaillé que très peu d'inégalités de ce genre ( avec des

au dénominateur ) . :cry:

Bonne chance !

par **Olympus** » 06 Nov 2010, 14:05

Salut !

Yeah j'ai enfin réussi à trouver :zen:

Il nous suffira de montrer que

Ce qui est vrai car par AM-GM on a :

On somme cycliquement et on conclut avec

.

:lol3:

par **benekire2** » 06 Nov 2010, 16:04

Très élégant bouazza :lol3:

par **Olympus** » 06 Nov 2010, 16:15

benekire2 a écrit:Très élégant bouazza :lol3:

Merci Michaël :zen:

Inégalité

Inégalité

Qui est en ligne