Inégalité pas trop facile ?

[MMu]

Montrer que
où sont des rééls non-négatifs. ...

[aviateur]

Bonjour
On met tout à droite et on multiplie par 64, l'inégalité est équivalente à
où f est un polynome homogène symétrique de degré 6.
Alors on peut supposer sans restreindre la généralité que .

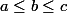
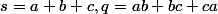
Posons et
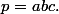
Un calcul montre que


Si s et q sont fixés alors p est minimum quand b=c=1. Cela se démontre assez facilement et je le laisse en exo.
Donc pour p et q fixés, puisque f(a,b,c) est une fonction affine de p et que le coeff de p est positif alors f(a,b,c) est minimum quand p est minimum donc quand b=c.
Vu l'homogénéité on peut supposer que b=c et donc on est amené à chercher le minimum de g(a)=f(a,1,1)
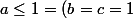Or
Le minimum est atteint en a=0.
Ce qui démontre l'inégalité avec égalité quand l'un 3 nombres est nul et les deux autres égaux.