D'après des dires, certains sont en manque d'olympiades. :we: ...
Pour
Bonne chance.
Thomas G :zen:
Inégalité pas trop complexe ...
18 messages
- Page 1 sur 1
inégalité pas trop complexe ...
par nekros » 13 Juil 2006, 00:34
Salut,
D'après des dires, certains sont en manque d'olympiades. :we: ...
Pour
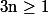
, montrer que pour toute famille _{1\le i \le n}})
de 
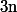
nombres réels strictements positifs, on a :
(\frac{1}{a_1}+...+\frac{1}{a_n}) \ge n^2})
Bonne chance.
Thomas G :zen:
D'après des dires, certains sont en manque d'olympiades. :we: ...
Pour
Bonne chance.
Thomas G :zen:
par aviateurpilot » 13 Juil 2006, 00:52
moyen arithmetique 
moyen geometrique
on a pour_{1\le k\le n})
et (>0)
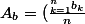^n\ge\bigprod_{k=1}^na<br />b_k=B_b)
donc
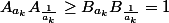
donc^n(\frac{\frac{1}{a_1}+...\frac{1}{a_n}}{n})^n\ge 1)
donc(\frac{1}{a_1}+...\frac{1}{a_n}) \ge n^2)
on a pour
donc
donc
donc
par Mikou » 13 Juil 2006, 10:17
L'inégalité de cauchy schwarz donne pour tout 
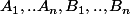
reels
:
 \times ( {B_1}^2 + ... +{B_n}^2) \geq (A_1 B_1 + ... A_n B_n )^2)
En prenant
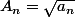
et 
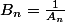
On retrouve donc(\frac{1}{a_1} + .. + \frac{1}{a_n} ) \geq ( sqrt{a_1} \times \frac{1}{\sqrt{a_1}} .... )^2)
soit finalement(\frac{1}{a_1} + .. + \frac{1}{a_n} ) \geq n^2)
:
En prenant
On retrouve donc
soit finalement
par aviateurpilot » 13 Juil 2006, 12:37
si _{1\le i\le n})
croissante et _{1\le i\le n})
décroissantes alors:
(b_1+...+b_n)\ge n\bigsum_{i=1}^na_ib_i)
on suppose que est croissante
et on pose
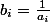
qui est décroissante
donc(b_1+...+b_n)\ge n\bigsum_{i=1}^na_ib_i=n\bigsum_{i=1}^n1=n^2)
on suppose que
et on pose
donc
par nekros » 13 Juil 2006, 12:46
salut aviateurpilot et Mikou,
Aviateurpilot,
Je ne suis pas bien réveillé : d'où vient la première inégalité. :dodo:
Sinon, j'ai posté ma solution pour le polynôme, si tu veux y faire un tour...
Je poserai 2 ou 3 exos sympas par semaine.
Au fait, t'es sûr que t'es en terminale !!
Je te donnerai un niveau math sup. :we:
Thomas G :zen:
Aviateurpilot,
Je ne suis pas bien réveillé : d'où vient la première inégalité. :dodo:
Sinon, j'ai posté ma solution pour le polynôme, si tu veux y faire un tour...
Je poserai 2 ou 3 exos sympas par semaine.
Au fait, t'es sûr que t'es en terminale !!
Je te donnerai un niveau math sup. :we:
Thomas G :zen:
par aviateurpilot » 13 Juil 2006, 12:56
nekros a écrit:Au fait, t'es sûr que t'es en terminale !!
Je te donnerai un niveau math sup.
je te jure
je suis encore en terminal
par aviateurpilot » 13 Juil 2006, 13:10
je l'ai vu dans le cour
je l'ai vu l'année derniere
...des moyens...
)
je l'ai vu l'année derniere
par aviateurpilot » 13 Juil 2006, 13:18
tu ne connais pas ça?
tu es en quel niveau ?
moi j'ai vu ça en 2eme année du lycée
tu es en quel niveau ?
moi j'ai vu ça en 2eme année du lycée
par nekros » 13 Juil 2006, 13:40
Le niveau en France au lycée est plus bas que celui du Maroc.
Je l'ai démontré par récurrence.
Sinon l'année prochaine je serais en licence de mathématiques.
Thomas G :zen:
Je l'ai démontré par récurrence.
Sinon l'année prochaine je serais en licence de mathématiques.
Thomas G :zen:
par Chimomo » 13 Juil 2006, 14:47
L'inégalité arithmético-géométrique peut se démontrer en deux lignes (une démo assez sympa).
par Chimomo » 13 Juil 2006, 17:09
La fonction ln est conave (évident). Donc 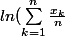 <= \displaystyle\sum_{k=1}^{n}\frac{ln(x_{k})}{n}=ln((\prod_{k=1}^{n}x_{k})^{1/n}))
On passe à l'exponentielle et c'est fini
On passe à l'exponentielle et c'est fini
par nekros » 13 Juil 2006, 18:17
Ok merci.
ln est concave car sa dérivée seconde est négative. (juste pour ceux qui ne le savaient pas)
Thomas G :zen:
ln est concave car sa dérivée seconde est négative. (juste pour ceux qui ne le savaient pas)
Thomas G :zen:
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :