Inégalité - Nombres complexes

[Zweig]

Salut,

Soit un nombre complexe vérifiant . Montrer qu'alors :

[CENTER][/CENTER]

[ThSQ]

Dans la catégorie "solution bestiale horrible" :

x = |1+z|
...
min et max de

[ThSQ]

Pour les amateurs d'ineg complexe :

des complexes non tous nuls

Mq on peut trouver une partie A de {1..n} telle que

Le '>' (ou lieu de >= est particulièrement intéressant ...)

Pour les plus courageux : est la meilleure constante

[ffpower]

Hey,c est un lemme du rudin ca :we: ...Bon pas pour l optimalité par contre..mais ca marcherait pas par hasard en prenant pour zi des racines n-emes de l unité?
Au passage,ca m a pas l air d etre optimal pour n=1 en tout cas^^

[ThSQ]

Ah ? Intéressant. Lequel de Rudin ? Il s'en sert pour montrer quoi ?

(Je l'ai eu en colle l'an dernier)

(elle est pas optimale pour n=0 non plus )

[Zweig]

Oui ThSQ, j'ai utilisé la même méthode :we: ...

[ThSQ]

Pas de méthode plus intelligente alors ?

ffpower ? J'aimerais bien savoir ce que Rudin fait avec cette ineg, stp.

[ffpower]

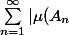yep,me voila.Donc,c est dans le rudin d'analyse complexe.Ca permet de montrer qu'une mesure complexe (=application des boreliens d un espace X dans C qui est sigma-additive) est a variation bornée,au sens suivant.On note le sup de ,ou est une partition(borelienne) de A(le sup se fait donc sur les partitions).On dit que est la variation de .On montre que est une mesure positive(facile).Le lemme permet de montrer que c est en fait une mesure finie(exo interessant),alors qu a priori c était meme pas évident qu elle soit sigma-finie.Donc voila,ca permet de ramener l étude d une mesure complexe a celle de l étude d une mesure finie.Par exemple:
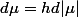
-Radon Nikodym permet d écrire ou h est une fonction borelienne de X dans les complexes de module 1.
-Si est une mesure signée(ie a valeurs réelles),alors elle est différence de mesures positives finies.La premiere,c est ,et l autre,bah je laisse deviner lol..Et si \mu est une mesure complexe quelconque,on peut se ramener a des mesures signées en regardant sa partie reelle et sa partie imaginaire.Du coup,au final,une mesure complexe est juste une CL de 4 probas..

Voila,je pense avoir répondu a ta question,si tu en veux plus,GO Rudin^^

[ThSQ]

Merci beaucoup ffpower ! Le passage dans C change beaucoup de chose.

J'aurais jamais imaginé que ce résultat serve en théorie de la mesure.

[ThSQ]

J'ai jeté un œil au Rudin ce midi à la docu. Toujours aussi bien le Rudin, tranchant comme l'acier ses démos. Dans son lemme il se contente de 1/6 comme minorant, c'est beaucoup plus facile ! (mais suffisant pour ce qu'il veut faire). Intéressant en tout cas.

[ffpower]

Je connais moi aussi que la demo avec le 1/6,mais dans la 3eme edition,il le fait avec 1/pi.Cela dit,pour ce qu il en fait,je prefere la demo avec le 1/6..
Sinon,moi aussi j aime bien le style du rudin.Toujours droit au but,c est classe..

[Nightmare]

Salut à tous :happy3:

Il me semble que l'optimisation est traitée dans un des Leichtam, à vérifier !

[ThSQ]

Merci pour vos réponses à tous les deux. Même en occaz chez Gibert où je passe pourtant régulièrement les Leichtman sont introuvables :(

[Nightmare]

Ils sont vraiment géniaux ces bouquins, ça aurait pu t'être d'ailleurs super utile pour toi ThSQ qui prépare les oraux (bien que je ne pense pas que tu en aies réellement besoin :lol3: )

Si tu les veux vraiment, je pourrai te les passer.

[ffpower]

Pour ma part,je préfere les cassini "oraux X-ens" aux Leitchman.Question de gout je suppose..

[Matt_01]

Salut tout le monde !

Pour j'ai l'impression que la majoration n'est pas vérifiée (je trouve 3,25). Où est l'erreur ? (Qui peut bien sûr venir de moi).

Edit : je trouve que la minoration n'est non plus pas vérifiée en prenant (qui donne )

[ThSQ]

Si tu les veux vraiment, je pourrai te les passer.

Waouh ça c'est grand ! C'est très très sympa mais je m'en voudrais de t'en priver. Grand merci de cette proposition :king2: