Inégalité, lvl1
Olympiades mathématiques, énigmes et défis
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 14 Déc 2011, 19:46
par nee-san » 14 Déc 2011, 19:46
bonsoir, voiçi une petite inégalité à montrer pour ceux qui veulent:
montrer que si
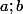
et

sont des réels positifs tels que
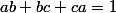
, on a:
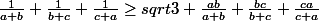
voila,

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 14 Déc 2011, 21:45
par Olympus » 14 Déc 2011, 21:45
Salut !
Après homogénéisation c'est équivalent à (a+b+c)²  3(ab+bc+ca), qui est évidente :happy2:
3(ab+bc+ca), qui est évidente :happy2:
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 26 Déc 2011, 14:42
par cheria2010 » 26 Déc 2011, 14:42
nee-san a écrit:bonsoir, voiçi une petite inégalité à montrer pour ceux qui veulent:
montrer que si
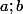
et

sont des réels positifs tels que
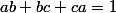
, on a:

voila,
salut .
on a :

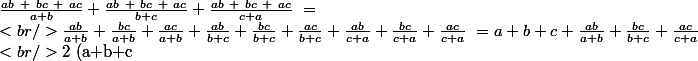^2= 2+a^2+b^2+c^2)
d'apres l'inegalite reordonnement :
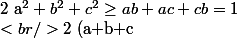^2\geq3\ \ alors\ \ a+b+c \geq\sqrt{3}\\<br />merci .)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités