Inégalité III : un classique
Olympiades mathématiques, énigmes et défis
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 15 Nov 2008, 13:44
par Mhdi » 15 Nov 2008, 13:44
Salut,
a, b et c sont des réels positifs. Montrer que :

@+
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 15 Nov 2008, 14:00
par Zweig » 15 Nov 2008, 14:00
Salut,
Sympa ton inégalité :++:
Alors déjà, ce qu'il y'a sous les racines me fait penser à Al-Kashi, c'est assez direct si on connait ce théorème, d'où mon idée d'essayer d'interprêter ça géométriquement :
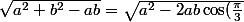+b^2})
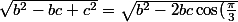+c^2})
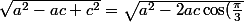+c^2})
Or d'après le théorème d'Al-Kashi :
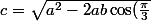+b^2})
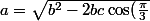+c^2})
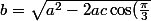+c^2})
L'inégalité demandée n'est autre que l'inégalité triangulaire.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 15 Nov 2008, 14:34
par Zweig » 15 Nov 2008, 14:34
Salut,
Sympa ton inégalité :++:
Alors déjà, ce qu'il y'a sous les racines me fait penser à Al-Kashi, c'est assez direct si on connait ce théorème, d'où mon idée d'essayer d'interprêter ça géométriquement :
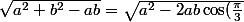+b^2})
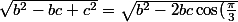+c^2})
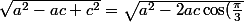+c^2})
Or d'après le théorème d'Al-Kashi :
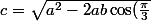+b^2})
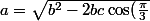+c^2})
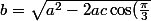+c^2})
L'inégalité demandée n'est autre que l'inégalité triangulaire.
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 15 Nov 2008, 14:55
par Mhdi » 15 Nov 2008, 14:55
Or d'après le théorème d'Al-Kashi : c = \sqrt{a^2 -2ab\cos(\frac{\pi}{3})+b^2} a = \sqrt{b^2 -2bc\cos(\frac{\pi}{3})+c^2} b = \sqrt{a^2 -2ac\cos(\frac{\pi}{3})+c^2}
D'après ce que tu viens d'écrire, on peut déduire angle(a,b)=angle(b,c)=angle(c,a)=pi/3, ce qui suppose que a=b=c. Or ce n'est pas toujours le cas !
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 15 Nov 2008, 14:56
par Zweig » 15 Nov 2008, 14:56
Oui je viens de voir ça ; cela dit, je pense que t'es trompé dans ton inégalité, dans le membre de droite ce serait plutôt +ac et dans ce cas on a :
http://img388.imageshack.us/my.php?image=mehdinz2.pngavec

,

et

On conclut comme précédemment.
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 15 Nov 2008, 15:13
par Mhdi » 15 Nov 2008, 15:13
Je pense aussi que l'exercice est erroné. C'est pourquoi j'ai posté ici ^^. Toutefois, si on démontre que l'inégalité est valable pour +ac on peut le démontrer aussi pour -ac...mais ça n'a pas vraiment de sens.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 15 Nov 2008, 15:14
par Zweig » 15 Nov 2008, 15:14
Bah, l'inégalité si c'est -ac n'est vraie que si a = b = c d'après ce que j'ai montré plus haut.
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 15 Nov 2008, 15:43
par Mhdi » 15 Nov 2008, 15:43
Tu as montré que si a=b=c, l'inégalité est vérifiée, non?
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 15 Nov 2008, 19:07
par lapras » 15 Nov 2008, 19:07
Mais, tout triplet de réel (a,b,c) ne correspond pas aux côtés d'un triangle !?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 15 Nov 2008, 19:11
par Zweig » 15 Nov 2008, 19:11
Pour la deuxième inégalité, si, car seulement a et b forment les côtés d'un triangle (c forme un deuxième triangle), donc il n'y a pas de soucis, par contre il est vrai que pour la première inégalité, cela ne marche pas
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 15 Nov 2008, 19:43
par Mhdi » 15 Nov 2008, 19:43
@Zweig :

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités