Indicatrice d'Euler
14 messages
- Page 1 sur 1
j ai une idée de demo.
cela revient a montrer que les produits de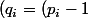/p_i)) sont denses dans [0,1].
sont denses dans [0,1].
si on paritionne cet intervalle en n intervalles on voit clairement qu il existe un produit dans le dernier intervalle. il existe un k tel que la multiplication de tout nombre du dernier intervalle ne se retrouve pas dans l avant-avant dernier intervalle. on multiplie alors notre produit par autant de necessaire a le faire basculer dans l avant dernier intervalle ( c est possible car le produit des
necessaire a le faire basculer dans l avant dernier intervalle ( c est possible car le produit des 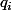 tends vers 0)
tends vers 0)
on repete l operation par recurence et on voit qu il existe un produit dans toutes les cases. comme on a pris n quelconque cela "démontre" le résultat.
excusez moi si ce n est pas tres formel, j avais un peu la fleme.j espere ne pas avoir fait (trop) d erreurs.
cela revient a montrer que les produits de
si on paritionne cet intervalle en n intervalles on voit clairement qu il existe un produit dans le dernier intervalle. il existe un k tel que la multiplication de tout nombre du dernier intervalle ne se retrouve pas dans l avant-avant dernier intervalle. on multiplie alors notre produit par autant de
on repete l operation par recurence et on voit qu il existe un produit dans toutes les cases. comme on a pris n quelconque cela "démontre" le résultat.
excusez moi si ce n est pas tres formel, j avais un peu la fleme.j espere ne pas avoir fait (trop) d erreurs.
jeancam a écrit:j ai une idée de demo.
cela revient a montrer que les produits desont denses dans [0,1].
si on paritionne cet intervalle en n intervalles on voit clairement qu il existe un produit dans le dernier intervalle. il existe un k tel que la multiplication de tout nombre du dernier intervalle ne se retrouve pas dans l avant-avant dernier intervalle. on multiplie alors notre produit par autant denecessaire a le faire basculer dans l avant dernier intervalle ( c est possible car le produit des
tends vers 0)
on repete l operation par recurence et on voit qu il existe un produit dans toutes les cases. comme on a pris n quelconque cela "démontre" le résultat.
excusez moi si ce n est pas tres formel, j avais un peu la fleme.j espere ne pas avoir fait (trop) d erreurs.
Ca a l air de marcher :++:
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
