Groupe
Olympiades mathématiques, énigmes et défis
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 14 Mar 2019, 13:58
par MMu » 14 Mar 2019, 13:58
Soit

un groupe multiplicatif et soient
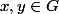
tels que
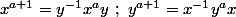
où

est un entier positif.
Est ce qu'on a toujours
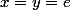
(élément neutre) ..


-
dereck
- Messages: 1
- Enregistré le: 30 Mar 2019, 20:56
-
 par dereck » 30 Mar 2019, 21:00
par dereck » 30 Mar 2019, 21:00
MMu a écrit:Soit

un groupe multiplicatif et soient
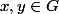
tels que
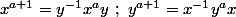
où

est un entier positif.
Est ce qu'on a toujours
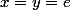
(élément neutre) ..


Bon je pense que tu devrai quantifier le problème,
Mais si cette relation est vrai pour tout a , alors elle est en particulier pour a=0 donc on conclut
-
mathelot
 par mathelot » 30 Mar 2019, 21:25
par mathelot » 30 Mar 2019, 21:25
pfff
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 01 Avr 2019, 05:10
par MMu » 01 Avr 2019, 05:10
dereck a écrit: MMu a écrit:Soit

un groupe multiplicatif et soient
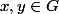
tels que
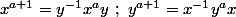
où

est un entier positif.
Est ce qu'on a toujours
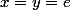
(élément neutre) ..


Bon je pense que tu devrai quantifier le problème,
Mais si cette relation est vrai pour tout a , alors elle est en particulier pour a=0 donc on conclut
Tu n'as rien compris ...

-
ffback
- Membre Relatif
- Messages: 101
- Enregistré le: 08 Mar 2016, 19:54
-
 par ffback » 16 Avr 2019, 14:21
par ffback » 16 Avr 2019, 14:21
En itérant la première relation
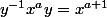
on obtient pour tout

que
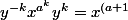^k})
, On applique pour
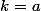
. Notant
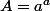
on déduit donc en particulier que
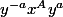
commute avec

. En utilisant ce fait suivi de la deuxième relation
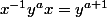
on obtient:
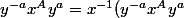x=(x^{-1}y^{-a}x)x^{A}(x^{-1}y^{a}x)=y^{-(a+1)}x^{A}y^{a+1})
,
d'ou on conclut que

commute avec
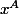
.
En repartant de
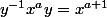
qu'on éleve à la puissance

, ça donne
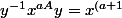A})
, donc
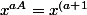A})
, et donc
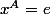
, c'est à dire
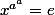
. Puis en réutilisant de nouveau la formule
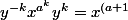^k})
avec
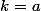
on déduit qu'on a aussi
^a}=e)
. Et puisque
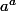
et
^a)
sont premiers entre eux, on conclut que

, et donc

aussi.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités




un groupe multiplicatif et soient
tels que
où
est un entier positif.
(élément neutre) ..

un groupe multiplicatif et soient
tels que
où
est un entier positif.
(élément neutre) ..
