Générateurs d'un groupe
Olympiades mathématiques, énigmes et défis

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Nov 2010, 15:35
par Ben314 » 26 Nov 2010, 15:35
Salut,
Si on parle de "structures algébriques", que pouvez vous dire d'un groupe
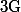
(à priori non commutatif)
engendré par deux éléments

et
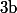
tels que
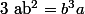
et
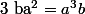
? (exercice du Querré : sans indics)
Bon courage...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 26 Nov 2010, 16:44
par Doraki » 26 Nov 2010, 16:44
A mon avis soit il est fini soit il est infini.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 26 Nov 2010, 17:07
par ffpower » 26 Nov 2010, 17:07
Doraki a écrit:A mon avis soit il est fini soit il est infini.
Je ne suis pas d'accord, cette assertion ne me semble pas du tout claire.
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 26 Nov 2010, 18:03
par Euler07 » 26 Nov 2010, 18:03
Salut, comme j'ai fini ce chapitre et même si je suis trop jeune pour répondre je dirais que dans ce cas là a=b=e

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Nov 2010, 18:12
par Ben314 » 26 Nov 2010, 18:12
Doraki a écrit:A mon avis soit il est fini soit il est infini.
As tu
UNE PREUVE ? :ptdr:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Nov 2010, 18:13
par Ben314 » 26 Nov 2010, 18:13
Euler 07 a écrit:Salut, comme j'ai fini ce chapitre et même si je suis trop jeune pour répondre je dirais que dans ce cas là a=b=e
As tu
une preuve ? :hein:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Nov 2010, 18:13
par Ben314 » 26 Nov 2010, 18:13
Doraki a écrit:A mon avis soit il est fini soit il est infini.
As tu
une preuve ? :ptdr:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 26 Nov 2010, 18:14
par Euler07 » 26 Nov 2010, 18:14
Oui mais je te sens pas assez convaincu :/
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 26 Nov 2010, 18:24
par Doraki » 26 Nov 2010, 18:24
Je trouve aussi que a=b=e.
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 26 Nov 2010, 18:28
par Euler07 » 26 Nov 2010, 18:28
Doraki a écrit:Je trouve aussi que a=b=e.
A cool ça serait bien si cela est vrai !! :ptdr:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 26 Nov 2010, 18:37
par Doraki » 26 Nov 2010, 18:37
Je te laisse le plaisir de vérifier ma preuve :
bbaaba = baaabba = baabbbaa = baabbaaab = aaabbbaaab = aaaabbaab = abaabaab =
abaaaaabb = abaaaabbba = abaaabbbaba = abbaabbaba = abbabbbaaba = abbabbaaabba = abbbbbaaaabba = abbbbaaabaabba = ababbaabaabba = ababbaaaaabbba = ababbaaaaaabb = ababbaaabaab = ababbbaaaab = abaabbaaab = abaabbbaa = abaaabba = abbaaba = bbbaaaba =
babbaa
donc abba = baab,
abbaba = baabba = aaabbba = aaaabb = abaab = aabba = abbbaa
donc ab = ba
aaab = baa = aba = aab
donc a = e
bb = abb = bbba = bbb
donc b = e
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 26 Nov 2010, 18:39
par Euler07 » 26 Nov 2010, 18:39
Ah c'est un peu comme ça que j'ai procédé mais pas avec autant de lettre :p
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 26 Nov 2010, 18:55
par ffpower » 26 Nov 2010, 18:55
Ma version :
On a
1)
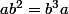
2)
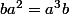
2) se réécrit
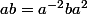
. En utilisant 1) sous la forme
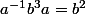
, on obtient
^3=a^{-1}b^2a)
puis
^9=b^4)
. Donc
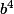
commute avec
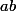
, donc avec

.
D'autre part, si on réécrit plutot 2) sous la forme
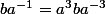
et qu'on utilise 1) sous la forme
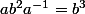
, on obtient de la même maniere
^8=b^{27})
, et donc que
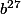
commute avec

.
Finalement,

commute avec

et on conclut aisément.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Nov 2010, 20:39
par Ben314 » 26 Nov 2010, 20:39
Bien joué à tout les deux.
Ma méthode perso :
b=_{(1)}a^2(b^{12}a)b=a(ab^{12})ab=_{(1)}a(b^{18}a)ab=(ab^{18})a^2b=_{(1)}(b^{27}a)a^2b=b^{27}(a^3b)=_{(2)}b^{27}(ba^2)=b^{28}a^2)
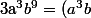b^8=_{(2)}ba^2b^{8}=ba(ab^8)=_{(1)}ba(b^{12}a)=b(ab^{12})a=_{(1)}b(b^{18}a)a=b^{19}a^2)
Donc
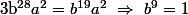
puis
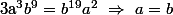
et enfin
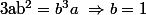
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 26 Nov 2010, 23:23
par Imod » 26 Nov 2010, 23:23
Comme je suis un peu la mémoire du forum :
groupe Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités