Fraction "successives".
49 messages
- Page 2 sur 3 - 1, 2, 3
Re: Fraction "successives".
Géométriquement c'est complètement évident si on connait la formule de Pick . On considère le triangle ABC avec A(0;0) , B(a;b) et C(c;d) dans le plan rapporté à un repère orthonormé . Les conditions imposées disent simplement que le triangle rencontre les nœuds du quadrillage uniquement en A , B et C ( aucun point à l'intérieur ) . Comme l'aire du triangle vaut (ad-bc)/2 , la formule de Pick permet de conclure .
Imod
Imod
Re: Fraction "successives".
Sauf erreur, ça ne donne pas complètement l'équivalence vu que le fait qu'il n'y ait pas de fractions p/q telles que q<max(b,d) entre a/b et c/d, ça implique qu'il n'y a pas de point à coordonnées entières dans le triangle ABC mais ce n'est pas équivalent. (ou alors j'ai raté quelque chose...)
Mais bon, c'est pas bien gênant vu que justement l'implication que ça démontre clairement, à savoir "Si a/b et c/d sont successives alors bc-ad=1", ben c'est justement celle où j'avais pas de preuve rapide (l'autre sens est assez évident)
Mais bon, c'est pas bien gênant vu que justement l'implication que ça démontre clairement, à savoir "Si a/b et c/d sont successives alors bc-ad=1", ben c'est justement celle où j'avais pas de preuve rapide (l'autre sens est assez évident)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Fraction "successives".
Un point à l'intérieur du triangle fournit un exemple de fraction fautive , non ?
Imod
Imod
Re: Fraction "successives".
Bonjour
@nogdim
Je me trompe peut être mais je pense que tu ne démontres pas la réciproque (le sens le plus difficile). C'est cela que je veux dire. D'ailleurs attendons que quelqu'un d'autre confirme ou infirme ta démo.
@nogdim
Il faut lire intégralement ce que j'ai écrit, Aviateur....
Je me trompe peut être mais je pense que tu ne démontres pas la réciproque (le sens le plus difficile). C'est cela que je veux dire. D'ailleurs attendons que quelqu'un d'autre confirme ou infirme ta démo.
Re: Fraction "successives".
Où serait la difficulté si on faisait ainsi:
soit une fraction donnée a/b
on peut construire l'ensemble des fractions de deltat (produit en croix) = 1
en les ordonnant de celle qui a le plus petit dénominateur possible puis la deuxième puis la troisième puis...
plus n augmente plus la fraction diminue
on peut construire l'ensemble des fractions de deltat = 2
en les ordonnant de celle qui le plus petit dénominateur puis la deuxième puis la troisième
Pour le moment on se fiche de construire des fractions réductibles, on les garde, on les laisse pour avoir le même ordre pour les deltats 1 et 2.
Pour chaque fraction d'ordre k on sait que:
celle en deltat 1 est inférieure à celle en deltat2
celle en deltat 2 d'ordre k+1 est à la fois de numérateur supérieur à deltat1 d'ordre k
et la fraction deltat 2 d'ordre k+1 est plus grande que la fraction deltat1 d'ordre k
Pour toute fraction deltat 2 j'aurais donc une fraction deltat 1 d'ordre -1 qui répond aux critères.
Pour les fractions deltat 2 qui n'existent pas car n'étant pas irréductibles, le soucis n'existe pas.
Pour les fractions deltat 1 non irréductibles, euh je sais pas.
reste à construire les successives, mais mathématiquement est-il difficile de les énumérer une par une?Et de les associer en bijection de deltat 1 à deltat 2?
Enfin moi j'en sais rien.J'ai juste lu ça dans ma boule.
soit une fraction donnée a/b
on peut construire l'ensemble des fractions de deltat (produit en croix) = 1
en les ordonnant de celle qui a le plus petit dénominateur possible puis la deuxième puis la troisième puis...
plus n augmente plus la fraction diminue
on peut construire l'ensemble des fractions de deltat = 2
en les ordonnant de celle qui le plus petit dénominateur puis la deuxième puis la troisième
Pour le moment on se fiche de construire des fractions réductibles, on les garde, on les laisse pour avoir le même ordre pour les deltats 1 et 2.
Pour chaque fraction d'ordre k on sait que:
celle en deltat 1 est inférieure à celle en deltat2
celle en deltat 2 d'ordre k+1 est à la fois de numérateur supérieur à deltat1 d'ordre k
et la fraction deltat 2 d'ordre k+1 est plus grande que la fraction deltat1 d'ordre k
Pour toute fraction deltat 2 j'aurais donc une fraction deltat 1 d'ordre -1 qui répond aux critères.
Pour les fractions deltat 2 qui n'existent pas car n'étant pas irréductibles, le soucis n'existe pas.
Pour les fractions deltat 1 non irréductibles, euh je sais pas.
reste à construire les successives, mais mathématiquement est-il difficile de les énumérer une par une?Et de les associer en bijection de deltat 1 à deltat 2?
Enfin moi j'en sais rien.J'ai juste lu ça dans ma boule.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Fraction "successives".
Rebonjour, (Exucses moi @beagle je n'ai pas lu ton texte)
mais je (re) propose une démonstration de la réciproque:
Sauf mention contraire les fractions considérées sont telle que
sont telle que  et
et 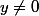
Soit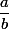 une fraction irréductible.
une fraction irréductible.
Soit
Considérons une fraction irréductible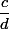 telle que
telle que
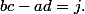
On sait qu'il existe une fraction telle que
telle que
 et on choisira
et on choisira 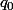 le plus petit possible.
le plus petit possible.
On a
-a (j q_0)=j) et il est facile de voir qu'il existe
et il est facile de voir qu'il existe 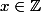 tel que
tel que

De plus) car
car 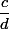 est irréductible.
est irréductible.
On pose alors avec
avec 
Posons et
et 
On veut que soit le bon candidat.
soit le bon candidat.
Déjà on a donc
donc 
Maintenant on a
(j k -x)= j k -x) Donc il faut que
Donc il faut que
 pour avoir
pour avoir 
Cette condition est donc aussi "en terme de y":
 convient
convient
Comparons et
et 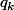
-(b k + q_0)=(j q_0 + b w + b j y)-(b + q_0 + b y)=(by + q_0)(j - 1) + b(w - 1))
Si alors on a évidemment
alors on a évidemment  et c'est terminé.
et c'est terminé.
Que se passe-t-il si
Dans ce cas on a=-b y -q_0\geq 1. i.e q_k<b.)
En conclusion la fraction répond à la question.
répond à la question.
mais je (re) propose une démonstration de la réciproque:
Sauf mention contraire les fractions considérées
Soit
Soit
Considérons une fraction irréductible
On sait qu'il existe une fraction
On a
De plus
On pose alors
Posons
On veut que
Déjà on a
Maintenant on a
Cette condition est donc aussi "en terme de y":
Comparons
Si
Que se passe-t-il si
Dans ce cas on a
En conclusion la fraction
Re: Fraction "successives".
Rebonjour
Exemple a/b=517/2017 et c/d=963/3757
bc-ad=j=2.
On cherche (p0,q0) par l'algorithme d"Euclide : p0/q0=223/770.
On calcule x: x=1. Puis k=1 donne une solution i.e
p_1/q_1=(p_0+ a)/(q_0+b)= 740/2887 (ici 2887<d=3557)
Exemple a/b=517/2017 et c/d=963/3757
bc-ad=j=2.
On cherche (p0,q0) par l'algorithme d"Euclide : p0/q0=223/770.
On calcule x: x=1. Puis k=1 donne une solution i.e
p_1/q_1=(p_0+ a)/(q_0+b)= 740/2887 (ici 2887<d=3557)
Re: Fraction "successives".
je crois que je me suis un peu fourvoyé sur les k et k+1
enfin bref
avec a/b = 517/2017
pour un delta de 1:
la k=1 première fraction est 223/870
c'est la plus élevée en valeur et elle a le min dénominateur
la k = 2, deuxième fraction est 740/2887
pour un delta de 2:
la k=1 première fraction est 446/1740 elle est de même valeur que la 1 de deltat -1
et en théorie n'existe pas car non irréductible, mais pour le compteur on la laisse
la k =2 deuxième fraction est 963/3757 elle est plus grande que la k=2 de deltat1
donc k=2 de delta 1 de valeur inf est de dénominateur plus petit
faur que je revois avec mes exemples a moi que j'avais pourquoi j'ai embrouillé.
Sinon je dis peut-être la même chose d'une autre manière que aviateur et nodgim, mais j'ai du mal à lire les maths niveau au-dela de la troisième.Et pour la démonstration je comptais sur mon binome mais il n'est pas là ce week-end.Le principe était on parle de fractions successives.Chiche alors on les numérote à parti d'un a/b fixé on a tous les delta 2 tous les deltas 1Et pour un k donné on doit bien savoir (mon binome?) laquelle est plus petite ou plus grande et avec quel dénominateur.Je pense qu'il fallait utiliser Péano dans cet exercice de fractions successives.
enfin bref
avec a/b = 517/2017
pour un delta de 1:
la k=1 première fraction est 223/870
c'est la plus élevée en valeur et elle a le min dénominateur
la k = 2, deuxième fraction est 740/2887
pour un delta de 2:
la k=1 première fraction est 446/1740 elle est de même valeur que la 1 de deltat -1
et en théorie n'existe pas car non irréductible, mais pour le compteur on la laisse
la k =2 deuxième fraction est 963/3757 elle est plus grande que la k=2 de deltat1
donc k=2 de delta 1 de valeur inf est de dénominateur plus petit
faur que je revois avec mes exemples a moi que j'avais pourquoi j'ai embrouillé.
Sinon je dis peut-être la même chose d'une autre manière que aviateur et nodgim, mais j'ai du mal à lire les maths niveau au-dela de la troisième.Et pour la démonstration je comptais sur mon binome mais il n'est pas là ce week-end.Le principe était on parle de fractions successives.Chiche alors on les numérote à parti d'un a/b fixé on a tous les delta 2 tous les deltas 1Et pour un k donné on doit bien savoir (mon binome?) laquelle est plus petite ou plus grande et avec quel dénominateur.Je pense qu'il fallait utiliser Péano dans cet exercice de fractions successives.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Fraction "successives".
Oui, dans ce sens là, ça marche, mais pas dans l'autre sens :Imod a écrit:Un point à l'intérieur du triangle fournit un exemple de fraction fautive , non ?
Imod
Si bc-ad>=2 alors il y a un point entier dans le triangle ce qui implique qu'il y a une fraction p/q avec q<max(b,d) entre a/c et b/d => O.K.
Mais dans l'autre sens, ça ne marche pas directement vu que l'existence d'une fraction p/q avec q<max(b,d) entre a/c et b/d ne garantie pas (*) l'existence d'un point entier dans le triangle (la condition q<max(b,d) est moins forte que celle disant que le point doit être en dessous de la droite (BC))
(*) ou alors, il y a un petit argument supplémentaire à fournir : j'ai pas cherché...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Fraction "successives".
nodgim a écrit:Pour tout k <= n , dk [b] = k*d1 et donc k/Bdk = k/Bkd1 = 1/Bd1.
Cette ligne là, je comprend pas trop d'où elle sort : Le fait que
nodgim a écrit:Si k > n, alors dk [B] < k*d1 et donc k / (B*dk) > k / (B*k*d1) = 1 / Bd1
Par contre ça c'est correct modulo que la notation avec des modulo en plein milieu d'une égalité, bien que ce soit plus ou moins compréhensible (je suppose que ton dk [B] désigne le reste de la division de dk par B) c'est archi. pourri et il faut s'en méfier comme la peste, en particulier du fait qu'il n'y a aucune relation d'ordre compatible sur Z/nZ donc aucune façon de définir un truc du style
Faut bien te rendre compte que si tu prend comme définition que
(par contre je comprend pas à quoi ça te sert ton "si k>n" ni même qui est n là dedans).
Et, effectivement, par rapport au problème de départ avec A/B<C/D, si on suppose que B=max{B,D} et qu'il n'y a pas de fraction de dénominateur <B entre les deux, ça prouve que C/D=c_1/d_1 et donc que BC-AD=1.
On peut traiter le cas D=max{B,D} en disant simplement qu'il suffit de remplacer A et C par leur opposé pour renverser l'inégalité.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Fraction "successives".
Rebonjour
Je reviens sur la démonstration de @nogdim que j'ai dû mal à comprendre mais surtout
j'aimerais savoir si elle répond aux questions suivantes.
La fraction c_1/d_1 ne me pose pas de problème.
1. Mais les fractions c_k/d_k construites à partir de c_1/d_1 .
Qu'est ce que cela veut dire ajouter c_k= k c_1 (modul a) et d_k=k d_1 modulo b
je pense qu'il faut ajouter x a à l'un et x b à l'autre?
2. A part k=1, les c_k et d_k sont-ils premiers entre -eux?
Je n'en vois nullement l'explication.
si c_k/d_k se réduit, d_1 peut être plus grand que que le dénominateur de la fraction réduite.
Ce point là est tout de même essentiel pour que la démonstration soit valide.
3. Il y a des fractions oubliées c/d qui ne sont pas de la forme c_k/d_k de la démonstration.
Cela m'a intrigué dès le départ.
En fait je n'ai rien compris du tout c'est trop nébuleux dans sa forme.
Mais je pense que ma démonstration est la bonne. Au moins s'il y a une erreur, ce qui peut arriver, cela sera plus facile à voir.
Je reviens sur la démonstration de @nogdim que j'ai dû mal à comprendre mais surtout
j'aimerais savoir si elle répond aux questions suivantes.
La fraction c_1/d_1 ne me pose pas de problème.
1. Mais les fractions c_k/d_k construites à partir de c_1/d_1 .
Qu'est ce que cela veut dire ajouter c_k= k c_1 (modul a) et d_k=k d_1 modulo b
je pense qu'il faut ajouter x a à l'un et x b à l'autre?
2. A part k=1, les c_k et d_k sont-ils premiers entre -eux?
Je n'en vois nullement l'explication.
si c_k/d_k se réduit, d_1 peut être plus grand que que le dénominateur de la fraction réduite.
Ce point là est tout de même essentiel pour que la démonstration soit valide.
3. Il y a des fractions oubliées c/d qui ne sont pas de la forme c_k/d_k de la démonstration.
Cela m'a intrigué dès le départ.
En fait je n'ai rien compris du tout c'est trop nébuleux dans sa forme.
Mais je pense que ma démonstration est la bonne. Au moins s'il y a une erreur, ce qui peut arriver, cela sera plus facile à voir.
Re: Fraction "successives".
aviateur a écrit:Rebonjour
Je reviens sur la démonstration de @nogdim que j'ai dû mal à comprendre mais surtout
j'aimerais savoir si elle répond aux questions suivantes.
La fraction c_1/d_1 ne me pose pas de problème.
1. Mais les fractions c_k/d_k construites à partir de c_1/d_1 .
Qu'est ce que cela veut dire ajouter c_k= k c_1 (modul a) et d_k=k d_1 modulo b
je pense qu'il faut ajouter x a à l'un et x b à l'autre?
Ce n'est pas un ajout. Quand on a la solution Ad1-Bc1 = -1, pour obtenir -k, il suffit de multiplier d1 et c1 par k. Par ailleurs, comme d1 ne doit pas dépasser B, il faut bien lui donner la valeur modulo B. Et pour ck = k*c1, il faut bien, en contre partie de dk modulo B, lui donner la valeur ck modulo A.
2. A part k=1, les c_k et d_k sont-ils premiers entre -eux?
Je n'en vois nullement l'explication.
Aucune importance, puisque ça ne change pas la valeur de la fraction. (J'ai été très hésitant sur cet aspect avant de l'ignorer....)
si c_k/d_k se réduit, d_1 peut être plus grand que que le dénominateur de la fraction réduite.
Ce point là est tout de même essentiel pour que la démonstration soit valide.
Je ne comprends pas très bien: si d1 est plus grand que dk, ça nous arrange, non ? Ce qui est sûr, c'est que si dk < d1, ck/dk > c1/d1.
3. Il y a des fractions oubliées c/d qui ne sont pas de la forme c_k/d_k de la démonstration.
Cela m'a intrigué dès le départ.
En fait je n'ai rien compris du tout c'est trop nébuleux dans sa forme.
Mais pour n'importe quelle fraction c/d, il existe bien un Ad-Bc associé. Les fractions ignorées sont celles dont le dk est- plus grand que le B, hors contrainte de l'énoncé.
En revanche, pardon pour la forme, que Ben314 n'apprécie pas non plus. Je n'ai pas été formé au langage mathématique.
Mais je pense que ma démonstration est la bonne. Au moins s'il y a une erreur, ce qui peut arriver, cela sera plus facile à voir.
Re: Fraction "successives".
Ben314 a écrit:nodgim a écrit:Pour tout k <= n , dk [b] = k*d1 et donc k/Bdk = k/Bkd1 = 1/Bd1.
Cette ligne là, je comprend pas trop d'où elle sort .
Si k <= n, alors k*d1 < B puisque n*d1 < B < (n+1)B (c'est de là que sort le n). Tout ça pour en venir à ceci: Si k <= n, alors dk=k.d1= dk [B] car dk n'est pas tronqué par [B].
NB : Je n'ai pas évoqué le cas B non premier, car dans ce cas, dk peut diviser B, mais ça ne change rien, sauf à avoir des fractions réductibles.
Re: Fraction "successives".
Salut nodgim, je te fais un coucou en passant.
Je réponds juste à beagle, j'essaye de pas trop couper le fil.
Effectivement dans l'exemple que tu avais pris beagle, pour un ordre k donné, tu avais le dénominateur de delta 2 plus petit, et alors cela marchait d'aller chercher le k+1 de delta 1 pour avoir une fraction à la fois de plus petit dénominateur et plus petite que le k de delta 2
Sur l'exemple d'Aviateur, on pouvait garder le k, pour tout k delta 1 a numérateur plus faible et fraction plus petite que le k delta2.
Bon je vous laisse faut que je plante mes fraisiers, toujours pas fait...
Je te rends le fil de discussion nodgim.
Je réponds juste à beagle, j'essaye de pas trop couper le fil.
Effectivement dans l'exemple que tu avais pris beagle, pour un ordre k donné, tu avais le dénominateur de delta 2 plus petit, et alors cela marchait d'aller chercher le k+1 de delta 1 pour avoir une fraction à la fois de plus petit dénominateur et plus petite que le k de delta 2
Sur l'exemple d'Aviateur, on pouvait garder le k, pour tout k delta 1 a numérateur plus faible et fraction plus petite que le k delta2.
Bon je vous laisse faut que je plante mes fraisiers, toujours pas fait...
Je te rends le fil de discussion nodgim.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Fraction "successives".
Bonjour
@nogdim merci d'avoir répondu et d'accepter la contradiction.
J'essaye de comprendre où tu veux en venir, je comprends un peu mieux certain passage mais j'ai encore des problèmes.
Pour c1/d1 pas de problème et on a bien a/b<c1/d1.
Ensuite pour (c_k, dk)=(kc1,k d1) modulo quelque chose, cela ne peut être que
(c_k, dk)=(kc1,k d1) +x (a,b) (je ne vois pas autre chose)
En effet il faut b dk-a d_k=k. Pour le choix de x, je suppose que tu choisis x de sorte que

Mais alors ck d1-c1dk = x(ad1-bc1)=-k x .
Donc ck/dk>c1/d1 si x<0.
Si dk<d1 effectivement, x est négatif et on a bien x<0 et ck/dk>c1 /d1 ( là tu as raison mais sans explication on ne peut pas le voir)
Maintenant le cas x=0 et x>0 ne sont pas exclus a priori.
Donc on peut avoir c1/d1>=ck/dk.
Mais alors pourquoi le cas dk>d1 nous arrange??
@nogdim merci d'avoir répondu et d'accepter la contradiction.
J'essaye de comprendre où tu veux en venir, je comprends un peu mieux certain passage mais j'ai encore des problèmes.
Pour c1/d1 pas de problème et on a bien a/b<c1/d1.
Ensuite pour (c_k, dk)=(kc1,k d1) modulo quelque chose, cela ne peut être que
(c_k, dk)=(kc1,k d1) +x (a,b) (je ne vois pas autre chose)
En effet il faut b dk-a d_k=k. Pour le choix de x, je suppose que tu choisis x de sorte que
Mais alors ck d1-c1dk = x(ad1-bc1)=-k x .
Donc ck/dk>c1/d1 si x<0.
Si dk<d1 effectivement, x est négatif et on a bien x<0 et ck/dk>c1 /d1 ( là tu as raison mais sans explication on ne peut pas le voir)
Maintenant le cas x=0 et x>0 ne sont pas exclus a priori.
Donc on peut avoir c1/d1>=ck/dk.
Mais alors pourquoi le cas dk>d1 nous arrange??
Re: Fraction "successives".
Ben314 a écrit:Oui, dans ce sens là, ça marche, mais pas dans l'autre sens...Imod a écrit:Un point à l'intérieur du triangle fournit un exemple de fraction fautive , non ?
Imod
Tu as raison , à vrai dire je ne m'étais pas occupé de ce sens qui est assez "évident" algébriquement . On peut y arriver quand même en considérant B' ou C' symétriques du point A par rapport à B ou C et en utilisant Pick dans AB'C ou ABC' . C'est complètement artificiel , c'est uniquement si on souhaite rester dans le même mode .
Imod
PS : je n'ai pas regardé les démonstrations algébriques de Nodgim et Aviateur , c'est très mal .
Re: Fraction "successives".
Sinon, s'il y en a que ça intéresse, le résultat en question est parfaitement connu et il s'énonce en général en terme de voisins dans une suite de Faray (<- lien Wiki)
(bizarrement, sur wiki, ils énoncent le résultat mais ne proposent pas de preuve...)
(bizarrement, sur wiki, ils énoncent le résultat mais ne proposent pas de preuve...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Fraction "successives".
aviateur a écrit:Bonjour
@nogdim merci d'avoir répondu et d'accepter la contradiction.
J'essaye de comprendre où tu veux en venir, je comprends un peu mieux certain passage mais j'ai encore des problèmes.
Pour c1/d1 pas de problème et on a bien a/b<c1/d1.
Ensuite pour (c_k, dk)=(kc1,k d1) modulo quelque chose, cela ne peut être que
(c_k, dk)=(kc1,k d1) +x (a,b) (je ne vois pas autre chose)
En effet il faut b dk-a d_k=k. Pour le choix de x, je suppose que tu choisis x de sorte que
Mais alors ck d1-c1dk = x(ad1-bc1)=-k x .
Donc ck/dk>c1/d1 si x<0.
Si dk<d1 effectivement, x est négatif et on a bien x<0 et ck/dk>c1 /d1 ( là tu as raison mais sans explication on ne peut pas le voir)
Maintenant le cas x=0 et x>0 ne sont pas exclus a priori.
Donc on peut avoir c1/d1>=ck/dk.
Mais alors pourquoi le cas dk>d1 nous arrange??
Je te donne un exemple, tu vas comprendre tout de suite je crois.
5/8 - c/d :
5d-8c = -1 pour la fraction c/d) = 2/3.
5d-8c = -2 pour la fraction c/d = (2*2)/(2*3)=2/3.
5d-8c = -3 pour la fraction c/d = (3*2)/(3*3)=2/3 mais aussi pour (3*2-5)/(3*3-8)=1/1
1/1 est plus éloigné de 5/8 que 2/3. Ceci est dû au fait l'écart vaut -k/(B*d). Pour 2/3 : -3/(8*3) et pour 1/1 : -3/(8*1).
Tronquer d modulo B le ramène dans l'intervalle de contrainte mais éloigne forcément c/d de 5/8
Re: Fraction "successives".
Salut, bon c'est un niveau en-dessous mais chacun va où il peut, à sa vitesse,
pouvez-vous me dépanner d'un couple de fractions avec le delta 1 qui n'est pas irréductible, ou devient irréductible en ordre plus élevé.Merci.
pouvez-vous me dépanner d'un couple de fractions avec le delta 1 qui n'est pas irréductible, ou devient irréductible en ordre plus élevé.Merci.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Fraction "successives".
J'ai pas bien compris la question, mais si ce que tu appelle "le delta", c'est bc-ad (si les fraction sont a/b<cd) alors le fait que "le delta" soit égal à 1, ben ça implique que a/b (et c/d) sont irréductibles.
C'est le théorème de Bézout : deux entiers a et b sont premiers entre eux si et seulement si il existe deux entiers (relatifs) u et v tels que au+bv=1.
C'est le théorème de Bézout : deux entiers a et b sont premiers entre eux si et seulement si il existe deux entiers (relatifs) u et v tels que au+bv=1.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
49 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
