Formule d'optimisation de production

[mathmathou]

Bonsoir à tous,

Je m'appelle Mathias, j'ai 41, et les mathématiques et moi avons toujours été fâchés (3/20 au Bac C, mais c'était au siècle dernier), même si elles m'attirent.
Je suis surtout versé dans la programmation, qui nécessite pour l'algorithmie, plus de logique que de réelles mathématiques. Mais parfois, on tente de développer des outils et les équations manquent.

C'est en toute humilité que je me présente à vous ce soir, avec l'espoir que quelqu'un, peut-être, pourra m’aiguiller dans la bonne direction.

Je poste mon message dans la partie "défis" car cela me semble indiqué, mais si l'emplacement n'est pas adéquat, je suis certain qu'un modo sympa le déplacera :lol3:

Bref...

Comme je suis plus à l'aise avec les exemples, je vais tenter d'illustrer mon problème :

EXEMPLE SIMPLE :
Stock de composant A : 10 unités
Stock de composant B : 9 unités

Circuit 1 nécessite : 6A + 4B
Circuit 2 nécessite : 2A + 2B

Dans un cas comme celui-ci, INTUITIVEMENT, je suis capable de déterminer que la meilleure combinaison de production est :
1 circuit de type 1 + 2 circuits de type 2
car après production, mon stock de composant A est à 0, et il ne me reste qu'un seul composant B.

Pourquoi ? Parce que le nombre de combinaisons possible est très bas et que cela se calcule de tête facilement, même pour moi :zen:

[CENTER]-----------------------[/CENTER]

Je pense que vous l'avez deviné, je cherche à déterminer la meilleure combinaison de production, dans le but de minimiser mes stocks en fin de procédé.

Dans mon exemple c'est simple, mais si je corse le problème en passant de 2 à 3 composants, et de 2 à 3 circuits comme ceci :

EXEMPLE COMPLEXE:
Stocks de départ
Stock de composant A : 80
Stock de composant B : 70
Stock de composant C : 56

Assemblages possibles :
Circuit 1 nécessite : 5A + 4B + 2C
Circuit 2 nécessite : 4A + 5B + 3C
Circuit 3 nécessite : 2A + 4B + 5C

Dans ce cas là, je ne sais même pas par quel bout attaquer le problème :mur:

Je ne cherche pas à produire un max de 1, puis de 2 avec ce qui reste, puis de 3, je cherche la combinaison de circuits 1, 2 et 3 qui me laissera à la sortie les stocks les plus bas.

Je ne suis pas venu chercher une résolution de mon problème (il est plus complexe, puisque les composants sont au nombre de 7, et les circuits au nombre de 14), je cherche essentiellement à savoir de quelle manière on met en équation ce genre de problématique parce que... je sèche.

En même temps, je l'ai précisé en introduction... 3/20 au bac :hum:

Merci de m'avoir lu

Cordialement

Mathias

[chan79]

Bonjour
Tu veux que la somme des composants restants soit minimale ?

[mathmathou]

Bonjour
Tu veux que la somme des composants restants soit minimale ?

Bonjour Chan79, et merci d'avoir pris la peine de me lire et de me répondre.

A vrai dire, je ne sais trop quoi répondre à ta question car... je n'y ai pas pensé sous cet angle, je suppose qu'on pourrait effectivement le dire.

J'avais pensé que, dans l'idéal, la composition des stocks restante ne permettrait plus de produire ni le circuit 1, ni le 2, ni le 3.

Je ne sais pas si on peut poser cela comme ceci (ne riez pas si j’écris une grosse ânerie :we: ) :

Code: Tout sélectionner

Un circuit 1 = (5A + 4B + 2C)
Un circuit 2 = (4A + 5B + 3C)
Un circuit 3 = (2A + 4B + 5C)

Stock de composant A : 80
Stock de composant B : 70
Stock de composant C : 56

Pour consommer un maximum de composants (je ne sais pas formuler cela en termes matéhmatiques...), il nous faut produire :
X(5A + 4B + 2C) + Y(4A + 5B + 3C) + Z(2A + 4B + 5C)

avec

X(5A) + Y(4A) + Z(2A) = 80 (ou approchant, le restant étant un nombre entier)
X(4B) + Y(5B) + Z(4B) = 70 (ou approchant, le restant étant un nombre entier)
X(2C) + Y(3C) + Z(5C) = 56 (ou approchant, le restant étant un nombre entier)

Sont-ce 3 équations du premier degré à 3 inconnues ? Et si oui, peut-on raisonnablement les résoudre ?
Comment exprimer en termes mathématiques que "les stocks restants ne doivent plus permettre de produire 1, 2 ou 3 ?

Je ne cherche pas à produire la même quantité de circuits1, 2 et 3, je cherche à calculer
X circuit1 + Y circuit 2 + Z circuit 3 = stock insuffisant pour produire autre chose.

Je sens bien que mes explications sont "floues" et je m'en excuse

Amicalement

Mathias

[eriadrim]

Pour se genre de problème, il faut formaliser le problème mathématiquement avec les données que l'on a et ce que l'on veut.

Dans ce cas, les données que tu as ce sont les stocks des composants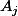 que l'on peut appeler 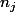. Nous avons aussi le nombre de composants que prend chaque circuit, on appellera donc le nombre de composants 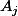nécessaire pour fabriquer le circuit .
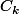Enfin, on cherche à déterminer le nombre de circuit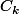 à produire que l'on appellera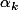

Après il faut poser les contraintes. Par exemple, dans notre cas, une contrainte pourrait être que l'on ne peut pas avoir de stock négatif :



On voudrait aussi maximiser le nombre de circuit produit (je pense) :

est maximum

On voudrait aussi minimiser le nombre de stocks restant :

est minimum

A partir de la tu as trois équations, reste plus qu'à les résoudre. Après le problème est que une solution optimale n'existe à priori n'existe pas (sauf si tu as beaucoup de chance). Mais il va falloir choisir si on préfère construire beaucoup de circuit et ne pas minimiser les stocks ou vice-versa.

EDIT :

J'avais pensé que, dans l'idéal, la composition des stocks restante ne permettrait plus de produire ni le circuit 1, ni le 2, ni le 3.

Si tu veux juste ça, un algorithme glouton devrait suffire, mais la solution ne risque pas d'être optimal

EDIT2 :

Il y a un autre problème, c'est que les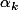 que l'on cherchent sont à priori entiers, et la recherche de solution devient plus compliqué.

[mathmathou]

Bonjour eriadrim et merci pour cette réponse,

Pour répondre à ta question et pour borner le problème, l'objectif principal est de minimiser les stocks.

Je sais qu'il n'y aura probablement pas de solution idéale avec stock = 0, mais le plus bas possible serait déjà pas mal.

Algorithme glouton ? Je me suis précipité sur Wikipedia, et c'est .... "effrayant".

Je suis désolé de vous avoir ennuyés avec mes problèmes, mais j'ai l'impression que la solution, qui doit sans doute exister, sera tellement compliquée (pour moi) qu'il me sera impossible de l'appréhender et de la traduire en code php. :lol3:

[eriadrim]

L'algorithme glouton est pratique mais ne permet pas de minimiser les stocks.
Pour faire simple, avec l'algorithme glouton, on va fabriquer le plus possible de circuit 1, quand on aura plus les stocks pour fabriquer le circuit 1, on fabrique plein de circuit 2 etc ...
Après le problème dans ce cas et d'une part que les stocks ne seront pas minimiser, mais surtout tu risque de ne pas fabriquer les derniers circuits de la listes. Mais le grand avantage est qu'il est très facile à mettre en oeuvre.

Pour en revenir à l'autre problème, si je me souviens bien, il existe déjà des programmes permettant de résoudre les équations (ou les approcher). Certains sont payants, mais il me semblent qu'il en existe des très performants et gratuits.

[chan79]

Pour le second exemple:
En maximisant le nombre total de circuits, on arrive à
9 circuits 1
1 circuit 2
7 circuits 3
il nous reste 18 composants (17 A, 1 B et 0 C)

Il peut y avoir d'autres solutions avec 17 circuits
---------------
En minimisant les stocks (il se trouve qu'on tombe aussi sur 17 circuits)
9 circuits 1
2 circuits 2
6 circuits 3
il reste 17 composants (15 A, 0 B et 2 C)

J'ai fait des boucles mais on peut être vite limité en augmentant le nombre de données

[nuage]

Salut,

le problème est connu, et fait l'objet de nombreuses recherches.

Tu peux chercher « programmation linéaire » en rajoutant éventuellement « méthode du simplex ».

Il y a une abondante littérature sur le sujet, j'espère que tu trouveras des solutions qui te conviennent.

[mathmathou]

Merci à tous pour vos réponses, et merci à nuage pour les deux pistes qu'il m'a données, qui relance mon "travail".

Bonne journée à tous

Amicalement


Mathias

[Dlzlogic]

Bonjour,
Sujet vraiment intéressant.
Juste une question, il s'agit de production, mais à aucun moment je n'ai lu que la "demande" entrait en ligne de compte.
A mon avis, ce problème est abordé de façon un peu trop théorique,

Pour se genre de problème, il faut formaliser le problème mathématiquement avec les données que l'on a et ce que l'on veut.

et j'appuie Eriadrim.
En d'autres termes, est-ce que toutes les "solutions" sont équivalentes, ou il y a d'autres critères plus réalistes et plus palpables, tels que les commandes ?