Fonction
Olympiades mathématiques, énigmes et défis
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Mai 2008, 19:17
par aviateurpilot » 03 Mai 2008, 19:17
salut, voila un exo (pas trop difficile)
trouver tt les focntions continue de
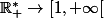
tel que
\in\mathbb{N}\times \mathbb{R}_+^*:\ \bigprod_{k=1}^{n}f(kx)<2008n^{2009})
:++:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 03 Mai 2008, 19:58
par ThSQ » 03 Mai 2008, 19:58
f(x) = 1 sinon contradiction à l'infini ? (et 2008 et 2009 sont là juste pour distraire !)
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 03 Mai 2008, 20:16
par ffpower » 03 Mai 2008, 20:16
Effectivement,en prenant x=c/n et en faisant tendre n vers l infini,on obtient f(c)=1
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Mai 2008, 20:22
par aviateurpilot » 03 Mai 2008, 20:22
oui, c'est ce que j'ai fait, (contradiction a l'infini)
mais j'ai pas pris
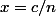
. tu px me dire comment t'a utilisé c/n
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 03 Mai 2008, 20:37
par ffpower » 03 Mai 2008, 20:37
Supposons f(c)>1 on a donc f>r>1 sur un voisinage de c.Si akx=kc/n>ac donc f(kx)>r,d ou
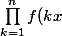\geq\prod_{k=an}^nf(kx)\geq r^{(1-a)n})
,d ou l absurdité
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Mai 2008, 20:44
par aviateurpilot » 03 Mai 2008, 20:44
voila, persque la meme chose que moi,:++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités