
Fonction
13 messages
- Page 1 sur 1
Re: fonction
Bonjour,
-f(y))(f(x+\sqrt{x^2-y^2})-f(x-\sqrt{x^2-y^2})) = 0)
-f(y))}{x-y}\frac{(f(x+\sqrt{x^2-y^2})-f(x-\sqrt{x^2-y^2}))}{2\sqrt{x^2-y^2}} =( \frac{\Delta f}{\Delta x})^2= 0)
À vu d’œil je dirais les fonctions constantes ?
À vu d’œil je dirais les fonctions constantes ?
Modifié en dernier par FLBP le 30 Aoû 2017, 15:04, modifié 1 fois.
Re: fonction
pas besoin de dérivés pour voir que certaines des solutions sont les fonctions constante en effet :
soit f une solution constante éventuel on a d'une part f(x) = c avec c un réel fixé et x un réel et de l'autre si on remplace dans l'équation fonctionnelle le terme-f(y)) devient
devient  (i.e. 0) et donc l'égalité est bien vérifié ! en revanche je doute que les fonctions constantes soit les seuls solution...
(i.e. 0) et donc l'égalité est bien vérifié ! en revanche je doute que les fonctions constantes soit les seuls solution...
soit f une solution constante éventuel on a d'une part f(x) = c avec c un réel fixé et x un réel et de l'autre si on remplace dans l'équation fonctionnelle le terme
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
Re: fonction
Soit 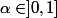 tel que
tel que 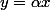
Nous avons que - f(\alpha x))(f(x + \sqrt{x^2-\alpha^2x^2})f(x - \sqrt{x^2-\alpha^2x^2})) = 0)
Donc soit = f(\alpha x)) , et\ou
, et\ou  = f(x - \sqrt{x^2-\alpha^2x^2}))
Dans le cas où la première condition est remplie :
 = f(\alpha x) = \beta)
avec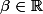
Dans le cas où la deuxième condition est remplie :
 = f(x - \sqrt{x^2-\alpha^2x^2}))
 = f(x - x\sqrt{1-\alpha^2}))
) = f(x(1 - \sqrt{1-\alpha^2})))
Si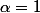 nous trouvons que
nous trouvons que  = f(x))
Sinon avec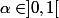 ces deux fonctions sont bijectives et continument dérivables :
ces deux fonctions sont bijectives et continument dérivables :
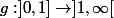
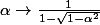
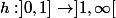
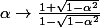
Si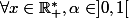 nous avons que
nous avons que 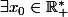 tel que
tel que x_0) alors :
alors :
) = f(x_0) = \gamma) avec
avec 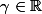 où
où) couvre les réels strictement positifs.
couvre les réels strictement positifs.
Donc = f(\alpha x) = \beta) \cup \lbrack(f(x) = f(x)) \cap (f(x_0h(\alpha)) = f(x_0) = \gamma)\rbrack \implies f(x) = \beta \cup f(x) = \gamma)
Avec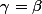 si les deux conditions sont remplies.
si les deux conditions sont remplies.
Donc je ne vois pas d'autres solutions que les fonctions constantes.
Nous avons que
Donc soit
Dans le cas où la première condition est remplie :
avec
Dans le cas où la deuxième condition est remplie :
Si
Sinon avec
Si
Donc
Avec
Donc je ne vois pas d'autres solutions que les fonctions constantes.
Re: fonction
Bonjour
Je n'ai pas cherché mais il me semble qu'on fait suite à : http://www.forum.math.ulg.ac.be/viewthread.html?SESSID=7ca889f8fe85b404acc0579594dd49d0&id=59315
D'autre part FLBP a proposé une solution , qu'en penses-tu ?
Imod
Je n'ai pas cherché mais il me semble qu'on fait suite à : http://www.forum.math.ulg.ac.be/viewthread.html?SESSID=7ca889f8fe85b404acc0579594dd49d0&id=59315
D'autre part FLBP a proposé une solution , qu'en penses-tu ?
Imod
Re: fonction
Non je n'ai pas compris sa solution , j'ai très vite décroché , mais ce n'est pas mon problème . Imagine que tu proposes une réponse à un problème de FLBP et qu'il te réponde : il n'y a vraiment personne ici 
On ne peut pas proposer un problème et rester muet tant qu'on n'a pas récupéré la solution qu'on espère : il y a un minimum de service après vente à assurer ( ce n'est que mon avis ) .
Imod

On ne peut pas proposer un problème et rester muet tant qu'on n'a pas récupéré la solution qu'on espère : il y a un minimum de service après vente à assurer ( ce n'est que mon avis ) .
Imod
Re: fonction
Bonjour
Supposons que l'on a une solution f non constante.
Soit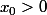 fixé. Et
fixé. Et \neq f(x_0)\})
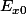 est non vide et supposons que (H)
est non vide et supposons que (H)
(H) : 0 est valeur d'adhérence de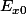
On a donc une suite dans
dans 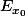 qui converge vers
qui converge vers  et
et
qui vérifie
=f(x_0-\sqrt{x_0^2-y_n^2}))
Par la continuité de f on en déduit que f a une limite en 0 et cette limite est 2f(x0).
Si tout vérifie l'hypothèse (H) alors f est constante et on a une contradiction.
vérifie l'hypothèse (H) alors f est constante et on a une contradiction.
Soit donc un élément qui ne vérifie pas (H). Posons
qui ne vérifie pas (H). Posons ) On a
On a 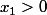 et f est constante sur
et f est constante sur 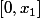
On peut peut être continuer ce raisonnement
Supposons que l'on a une solution f non constante.
Soit
(H) : 0 est valeur d'adhérence de
On a donc une suite
qui vérifie
Par la continuité de f on en déduit que f a une limite en 0 et cette limite est 2f(x0).
Si tout
Soit donc un élément
On peut peut être continuer ce raisonnement
Re: fonction
Je finis donc mon raisonnement
On a vu qu'il existe au moins un nombre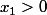 tel que f est constante sur
tel que f est constante sur 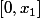 Soit
Soit  le plus grand nombre vérifiant cette propriété (il existe sinon f serait constante).
le plus grand nombre vérifiant cette propriété (il existe sinon f serait constante).
En particulier il existe une suite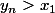 , qui tend vers
, qui tend vers  et vérifie
et vérifie \neq f(x_1))
On fixe d'abord un tel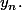
On a pour tout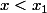 :
: =f(y_n^2-\sqrt{y_n^2-x^2}))
On vérifie facilement que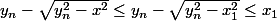
On obtient alors pour tout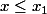 :
: =f(x_1))
Le raisonnement précédent étant valable pour tout on obtient par passage à la limite :
on obtient par passage à la limite :
Pour tout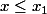 :
: =f(x_1))
Ceci implique que sur un intervalle du type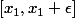 f est constante (et est égale à
f est constante (et est égale à ) ).
).
Cela contredit la définition de et termine la preuve (que seules les fonctions constantes sont solutions).
et termine la preuve (que seules les fonctions constantes sont solutions).
On a vu qu'il existe au moins un nombre
En particulier il existe une suite
On fixe d'abord un tel
On a pour tout
On vérifie facilement que
On obtient alors pour tout
Le raisonnement précédent étant valable pour tout
Pour tout
Ceci implique que sur un intervalle du type
Cela contredit la définition de
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

