Montrer que
Fonction
6 messages
- Page 1 sur 1
Bonjour,
Voici une tentative de solution.
1) Si on fait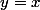 , on trouve que
, on trouve que
-2f(x)|\leq 2x^2)
2) On montre par récurrence que
-2^nf(x)|\leq (4^n-2^n) x^2)
C'est vrai pour ,
,  . Si la propriété est vraie pour
. Si la propriété est vraie pour  , on y remplace
, on y remplace  par
par 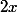
-2^nf(2x)|\leq (4^n-2^n)4 x^2)
et comme en multipliant la relation 1) par on a:
on a:
-2^{n+1}f(x)|\leq 2^{n+1}x^2)
Il vient que
-2^{n+1}f(x)|=|f(2^{n+1}x)-2^nf(2x)+2^nf(2x)-2^{n+1}f(x)|\leq (4(4^n-2^n)+2^{n+1})x^2=(4^{n+1}-2^{n+1})x^2)
3) On remplace par
par 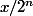 dans 2), on trouve que
dans 2), on trouve que
-2^nf(x/2^n)|\leq (1-\frac{1}{2^n})x^2)
Il ne reste plus qu'à faire tendre vers l'infini, en utilisant que pour
vers l'infini, en utilisant que pour  non nul,
non nul, =xf(x/2^n)/(x/2^n)) converge vers
converge vers =0) . (l'inégalité est triviale pour
. (l'inégalité est triviale pour  ).
).
Cordialement
Voici une tentative de solution.
1) Si on fait
2) On montre par récurrence que
C'est vrai pour
et comme en multipliant la relation 1) par
Il vient que
3) On remplace
Il ne reste plus qu'à faire tendre
Cordialement
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
